Entre deux nombre réels , il existe un nombre rationnel ....démonstration?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
maths-girl
- Membre Naturel
- Messages: 32
- Enregistré le: 03 Oct 2007, 16:21
-
 par maths-girl » 16 Oct 2008, 03:32
par maths-girl » 16 Oct 2008, 03:32
Salut,
J'arrive pas à démontrer ce qui suit:
Quelque soit x et y appartenant à l'ensemble des nombres réels R, tq xJ'ai besoin de votre aide!
Merci d'avance!!

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 16 Oct 2008, 06:29
par leon1789 » 16 Oct 2008, 06:29
Soit un entier n tel que

Trouver un rationnel q compris entre

et
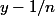
Indication : partie entière de
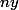
...
-
maths-girl
- Membre Naturel
- Messages: 32
- Enregistré le: 03 Oct 2007, 16:21
-
 par maths-girl » 22 Oct 2008, 00:53
par maths-girl » 22 Oct 2008, 00:53
Salut,
Au fait , j'ai eu la réponse , c'est comme ce qui suit:
On veut démontrer que
~qlq soit x et y , il existe r tq:
xx~prenons p=E(n.y) ( comment on a eu l'idée de considérer un nous élément p et de lui donner une telle epression?? :hein: )
Donc p/n=~Prenons r=(p-1)/n ( comment a-t-on encore l'idée d'une telle expression?)
~r-x=(p*1)/n-(2/n)-x
>y-(2/n)-x
~Puisque l'ensemble des réels R est archimédien , donc , il existe un n un nombre naturel entier,tq : n(y-x)>n ( encore une ligne maligne :hum: )
Donc y-(2/n)-x>0
Donc r-x>0 donc il existe un r tq: x
Voilà , je souffre à cause de ces questions entre les parenthèse....
Allez,, quelqu'un d'esprit mathématique qui peut aider un aussi modeste esprit que j'ai!!!
Merci,

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 22 Oct 2008, 08:20
par leon1789 » 22 Oct 2008, 08:20
maths-girl a écrit:~prenons p=E(n.y) ( comment on a eu l'idée de considérer un nous élément p et de lui donner une telle epression?? :hein: )
As-tu lu mon indication ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 22 Oct 2008, 08:26
par leon1789 » 22 Oct 2008, 08:26
maths-girl a écrit:Voilà , je souffre à cause de ces questions entre les parenthèse....
Allez,, quelqu'un d'esprit mathématique qui peut aider un aussi modeste esprit que j'ai!!!
La démo m'a l'air bien mal rédigée... (pour le peu qu'il y a démontrer !)
J'aurais fait comme cela :
pour tout
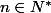
, on a
 \leq yn)
donc
/n \leq y)
Ensuite il existe
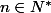
tel que
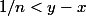
(car
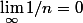
)
donc
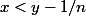
et finalement
/n \leq y)
où
/n)
est un rationnel.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 22 Oct 2008, 09:03
par leon1789 » 22 Oct 2008, 09:03
maths-girl a écrit:~Puisque l'ensemble des réels R est archimédien , donc , il existe un n un nombre naturel entier,tq : n(y-x)>n ( encore une ligne maligne :hum: )
surtout une ligne archi fausse !
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 22 Oct 2008, 10:42
par yos » 22 Oct 2008, 10:42
maths-girl a écrit:~prenons p=E(n.y) ( comment on a eu l'idée de considérer un nous élément p et de lui donner une telle epression?? :hein: )
On est d'autant plus impressionné par une preuve qu'on ne la comprend pas dirait-on.
J'appuie dans le sens de Leon1968 : c'est bien mal rédigé et les idées essentielles sont noyées.
Dessine un axe réel, place un 1/n pour un entier n>0, puis tous ses multiples k/n (
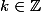
). Tu vois apparaître un tas de petits traits assez proches les uns des autres. Si aucun d'eux n'est entre x et y, c'est que tu n'as pas pris n assez grand.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités