Est ce que ce nombre peut etre rationnel

[rafik]

Bonjour,

Soit : ,

ce nombre peut il etre rationnel pour un certain n dans N ?

[Finrod]

Non.

Si tu prend n le plus petit entier tel qu'il soit rationnel alors on vérifie qu'il est aussi nécéssairement rationnel au rang n-1, c'est absurde.

[Imod]

C'est impossible mais la démonstration n'est pas simple :zen:

Imod

[Finrod]

Oui, l'idée que je donne nécéssite en effet d'aller chercher un peu plus loin.

Pour , j'ai. Mais après, je vois pas.

[rafik]

Il y a une façon assez simple pour le montrer, c'est de considérer un certain automorphisme d' une extension de Q qui contient ce nombre (un automorphisme laisse fixes les éléments de Q).

[Ben314]

Tient, je vient de penser à un début de preuve "élémentaire" :

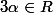
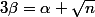
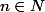
Si est racine d'un polynôme unitaire à coeff. entiers alors (où ) est racine de :

où , est unitaire de degrés et est de degrés au plus .
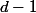
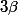
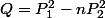
Donc est racine de qui est unitaire à coeff. entiers (de degrés 2d).

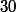
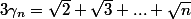
Comme est racine de unitaire à coeff. entiers, on en déduit (récurrence) que est racine d'un polynôme unitaire à coeff. entiers.
Donc, si c'est un quotient,... c'est un entier (je pense que c'est assez élémentaire et que... ça peut aider...)

Edit :
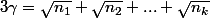
En fait, cela montre de façon élémentaire que, pour , si est un quotient, alors c'est un entier.

[rafik]

Voici une solution assez simple,

Si est un rationnel alors il est laissé fixe par un -automorphisme de toute extension de , et en particulier un -automorphisme de
, tel que on a alors

ainsi
ce qui contredit le fait que ce nombre soit un rationnel

[Finrod]

Je me pose deux questions, suite à celle-ci:

Pour une suite de nombres transcendant, quelqu'un aurait des idées ?

Peut-on pas aussi trouver une formule générale pour ?