Comment exprimer,
Merci.
Nombre rationnel
3 messages
- Page 1 sur 1
nombre rationnel
par Near » 09 Juil 2010, 21:52
Salut :we:
Comment exprimer,
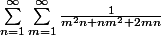
,sous la forme d'un nombre rationnel.
Merci.
Comment exprimer,
Merci.
par Ben314 » 09 Juil 2010, 23:29
Salut, en supposant qu'il y a une faute de frappe dans ton énoncé (tel qu'il est, la somme diverge...)
}\right))
(1) Pour
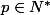
fixé et 
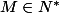
on a :
}\ <br />=\ \frac{1}{p}\sum_{m=1}^{M}\left(\frac{1}{m}\ -\frac{1}{m+p}\right)\ <br />=\ \frac{1}{p}\left(\sum_{m=1}^{M}\frac{1}{m}\ -\sum_{m=p+1}^{M+p}\frac{1}{m}\right))
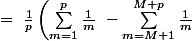\ \longrightarrow_{M\to\infty}\ <br />\frac{1}{p}\sum_{m=1}^{p}\frac{1}{m})
donc, en prenant
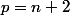
, il vient :
}\sum_{m=1}^{n+2}\frac{1}{m}\right)\<br />=\ \sum_{m=1}^{\infty }\left(\frac{1}{m}\sum_{n=\lambda_m}^{\infty}\frac{1}{n(n+2)}\right)\)
où )
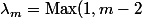(2) Pour
fixé et 
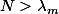
on a :
}\ <br />=\ \frac{1}{2}\sum_{n=\lambda_m}^{N}\left(\frac{1}{n}\ -\frac{1}{n+2}\right)\ <br />=\ \frac{1}{2}\left(\frac{1}{\lambda_m}+\frac{1}{ \lambda_m +1} -\frac{1}{N+1}-\frac{1}{N+2}\right)\ \longrightarrow_{N\to\infty}\ <br />\frac{1}{2}\left(\frac{1}{\lambda_m}+\frac{1}{ \lambda_m +1}\right))
donc
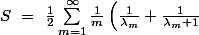<br />=\ \frac{1}{2}\left(\frac{3}{2}+\frac{3}{4}+\sum_{m=3}^{\infty }\frac{1}{m}\left(\frac{1}{m-2}+\frac{1}{m -1}\right)\right)<br />=\ \frac{1}{2}\left(\frac{9}{4}+\sum_{m=1}^{\infty }\frac{1}{m(m+2)}+\sum_{m=2}^{\infty }\frac{1}{m(m+1)}\right))
Or (cf (1) )}=\frac{1}{2}\left(1+ \frac{1}{2} \right)=\frac{3}{4}\)
et }=\sum_{m=1}^{\infty }\frac{1}{m(m+1)}-\frac{1}{2}=1-\frac{1}{2}=\frac{1}{2}\)
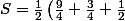donc=\frac{7}{4})
(aux erreurs de calcul prés...)
(1) Pour
donc, en prenant
(2) Pour
donc
Or (cf (1) )
donc
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Near » 10 Juil 2010, 12:08
Trop fort Ben :++: .
Merci beaucoup .
PS: j'ai vérifié l'énoncé c'était juste
:we:
Merci beaucoup .
PS: j'ai vérifié l'énoncé c'était juste
:we:
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :