Espaces normés
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 27 Aoû 2008, 10:26
par legeniedesalpages » 27 Aoû 2008, 10:26
Bonjour,
On considère un l'evn
)
avec
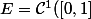,\mathbb{R}))
,
+ (f')^{2} (t)dt \)^{\frac{1}{2}})
.
Je bloque pour montrer qu'il existe
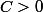
tel que pour tout
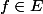
, on ait
)
.
Merci pour votre aide.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 27 Aoû 2008, 11:11
par yos » 27 Aoû 2008, 11:11
Salut.
En minorant
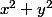
par 2xy, tu arrives à
\geq [f(b)^2-f(a)^2]^{\frac12})
avec a et b quelconques dans [0,1].
Puis
\geq |f(b)|-|f(a)|)
. Ensuite tu choisis a et b réalisant l'inf et le sup de f respectivement. Enfin tu trouves un C tel que
|-|f(a)|\geq C|f(b)|)
(il existe dés que f est non constante; si f est constante c'est trivial).
Je crois que ça marche.
-
totom
- Membre Naturel
- Messages: 33
- Enregistré le: 24 Oct 2007, 11:50
-
 par totom » 27 Aoû 2008, 11:19
par totom » 27 Aoû 2008, 11:19
Salut,
bonne idée mais ton C final dépend de f.
Il suffit de voir que f(b)-f(a) est supérieur à la norme sup, et c'est fini. A plus
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 27 Aoû 2008, 12:05
par Doraki » 27 Aoû 2008, 12:05
yos, ton C dépend pas mal de ta fonction f...
Il faut que a et b réalisent l'inf et le sup de f² respectivement.
Comme l'a dit yos, en minorant f²+f'² par +- 2ff' (choisir le signe selon le signe de a-b) sur [a,b] et 0 ailleurs, tu peux bien dire que N²(f) >= f²(b) - f²(a).
Ensuite tu minores f²+f'² par f²(a) pour dire que N²(f) >= f²(a).
Et de là tu peux conclure que 2.N²(f) >= f²(b) et donc t'obtiens ce que tu veux avec C = racine de 2.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 27 Aoû 2008, 15:34
par yos » 27 Aoû 2008, 15:34
Doraki a écrit:yos, ton C dépend pas mal de ta fonction f...
En effet, j'ai été un peu vite.
Ton truc a l'air bien.
 par legeniedesalpages » 28 Aoû 2008, 11:20
par legeniedesalpages » 28 Aoû 2008, 11:20
Un peu plus loin j'ai un souci aussi:
On considère le sous-espace fermé
= \{ f\in E:\ f(0)=0\})
. Il faut montrer que
 \rightarrow (\Bigint_0^1 (f')^2 (t) dt)^{\frac{1}{2}})
est une norme sur
)
équivalente à

.
Bon pour montrer que c'est une norme pas de problème, et on a
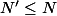
.
Ensuite j'ai du mal à trouver
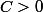
tel que
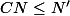
.
Edit: j'ai corrigé la définition de N'

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 11:23
par leon1789 » 28 Aoû 2008, 11:23
Pardon, mais quelle est la définition de N' ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 28 Aoû 2008, 13:05
par yos » 28 Aoû 2008, 13:05
Peut-être Cauchy-Schwarz appliqué à f' et 1 pour montrer que
^2\geq ||f||_\infty^2)
.
 par legeniedesalpages » 28 Aoû 2008, 18:27
par legeniedesalpages » 28 Aoû 2008, 18:27
yos a écrit:Peut-être Cauchy-Schwarz appliqué à f' et 1 pour montrer que
^2\geq ||f||_\infty^2)
.
En utilisant CS, j'ai
.N(1) = N(f'))
donc
dt|^2\leq N^2(f'))
ie
-f(0)|^2 \leq N^2(f'))
ie
|^2\leq N^2(f'))
et de là je ne vois pas comment en déduire que
^2\geq ||f||_\infty^2)
? Pourquoi faire intervenir la norme sup?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 28 Aoû 2008, 18:35
par Doraki » 28 Aoû 2008, 18:35
tu n'es pas obligé de faire l'intégrale sur le segment [0,1], tu peux t'arrêter à n'importe quel x entre [0,1] :
pour tout x,
^2 = \left(\int_0^x f' \right)^2 \leq \int_0^x {f'^2} \int_0^x 1 \leq x.{N'^2} (f) \leq {N'^2} (f))
 par legeniedesalpages » 28 Aoû 2008, 19:44
par legeniedesalpages » 28 Aoû 2008, 19:44
je ne saisis pas le lien qu'il y a entre
)
et
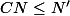
.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 28 Aoû 2008, 19:48
par Doraki » 28 Aoû 2008, 19:48
Ben ça sert si tu réussis à montrer qu'il existe C tel que C * N(f) <= || f || ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 28 Aoû 2008, 20:11
par yos » 28 Aoû 2008, 20:11
C'est pas N(f') mais N'(f). Ensuite tu utilises la relation de la question précédente.
 par legeniedesalpages » 29 Aoû 2008, 11:46
par legeniedesalpages » 29 Aoû 2008, 11:46
ok, on a
})
et de la relation précédente on sait qu'il existe
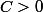
tel que
pour toute
)
,
})
,
et de ces deux inégalités, je dois en déduire qu'il existe
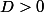
tel que
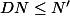
? :hein:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 29 Aoû 2008, 12:01
par Doraki » 29 Aoû 2008, 12:01
En fait nan la minoration de N(f) de la première question est inutile puisqu'on est en train de faire l'inverse.
T'as remarqué que
^2 = ||f||_2^2 + N'(f)^2)
?
Tu peux montrer qu'il existe C > 0 tel que
^2)
?
 par legeniedesalpages » 29 Aoû 2008, 12:06
par legeniedesalpages » 29 Aoû 2008, 12:06
ah oui d'accord avec,
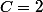
, merci.
Il y a encore un autre point qui me perturbe, c'est pour voir si
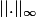
et

sont équivalentes.
Je pense que non, et je pensais avoir trouvé un contre-exemple, mais je me suis trompé. :mur:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 29 Aoû 2008, 12:29
par Doraki » 29 Aoû 2008, 12:29
Pour ça, regarde
 = \sin (n^2 x) / n)
Sinon, tu peux détailler ta preuve avec C=2 ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités