Espaces normés
25 messages
- Page 2 sur 2 - 1, 2
Doraki a écrit:En fait nan la minoration de N(f) de la première question est inutile puisqu'on est en train de faire l'inverse.
T'as remarqué que?
Tu peux montrer qu'il existe C > 0 tel que?
Bon pour ça c'est ok, je pense. J'ai montré que
On a ainsi
Doraki a écrit:Pour ça, regarde
Pour le calcul de
mais là je ne sais comment résoudre cette intégrale? :hein:
Comme N et N' sont équivalentes, c'est plus simple de regarder si N' et 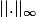 le sont.
le sont.
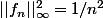
^2 = n^2 \int_0^1 cos^2(n^2 x)) , qui est équivalent à n²/2 quand n tend vers l'infini (pour résoudre l'intégrale, linéarise cos²x en (cos 2x + 1)/2 ).
, qui est équivalent à n²/2 quand n tend vers l'infini (pour résoudre l'intégrale, linéarise cos²x en (cos 2x + 1)/2 ).
Si les deux normes étaient équivalentes tu aurais donc une constante C > 0 telle que

C'est bien sur impossible.
Si les deux normes étaient équivalentes tu aurais donc une constante C > 0 telle que
C'est bien sur impossible.
25 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
