Probleme révisions pour MPSI

[Matt_01]

C'est ce qu'avait fait premièrement miikou non ?
Sinon, oui c'est la méthode qui me semble la plus simple :)

[miikou]

salut,
On arrive au meme resultat mais de facons un peu differentes.
La regle de l'hopitale est plus generale mais demande de verifier qq hypotheses au préalable.

[abcd22]

En faisant ça tu fais une inversion de limites, tu écris en fait:
, les inversions de limites ne marchent pas systématiquement, il faut justifier l'égalité.

[miikou]

En faisant ça tu fais une inversion de limites, tu écris en fait:
, les inversions de limites ne marchent pas systématiquement, il faut justifier l'égalité.

en les calculant peut etre ..

[Shaolan]

en les calculant peut etre ..

Nan, les interversions de limites ne se justifient pas aussi simplement...

Soit a un point de A, ou une borne de A.
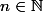
Si converge uniformément vers f sur A, et si pour tout , admet une limite en a,
Alors f admet une limite en a, et on a
On dit alors que l'on peut intervertir les limites, càd :


Mais vu que ce ne sont pas des suites de fonctions en l'occurrence, le théorème est peut-être différent...

[leon1789]

ro vous êtes intransigeants quand même :ptdr:
je prenais juste la partie régulière d'un DL a lodre 2( pour que la division par x² ne pose plus problème ), oui j'admets que l'utilisation de ' ~ ' était ici malheureuse :hein:

quitte à faire quelque chose de juste, autant prendre la bonne notation :id:

Et puis il y a aussi autre chose : ne pas écrire trop vite avant même de prouver que ces limites existent.

[leon1789]

en les calculant peut etre ..

si on a envie d'utiliser l'égalité Lim_1 = Lim_2 = ..., c'est qu'on ne sait pas calculer la Lim_1 ! ...

[leon1789]

la preuve que je propose (niveau TS, sans équivalent, ni DL, ni changement de variable, etc.) :


Or
donc existe et vaut 1
Comme
il vient existe et vaut 1/2

[La Boule]

On peut faire apparaitre quelque chose en multipliant numérateur et denominateur par , pas besoin de DL changement de variable et toute l'artillerie que notre futur sup n'est pas censé connaitre.

EDIT: Grillé ...