Intégrale recalcitrante
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
chwebij
- Messages: 5
- Enregistré le: 23 Juil 2008, 14:37
-
 par chwebij » 23 Juil 2008, 14:41
par chwebij » 23 Juil 2008, 14:41
bonjour
je me retrouve dans le cas d'une étude par perturbation avec cette intégrale à calculer
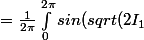 sin( w_1)-w_2 ) dw_1)
avec
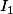
et
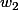
constants
et je suis pas foutu de la résoudre
j'ai cherché dans un handbook d'intégrales mais je ne trouve pas mon bonheur.
bon je suis sûr que la fonction s'exprime à partir d'une somme (genre fonction de Bessel) mais bon: je bloque!
si quelqu'un à une idée?
je vous remercie d'avance
ps: les logiciels de calcul formel n'ont rien donné (Maple et le site Integrator)
 par busard_des_roseaux » 23 Juil 2008, 15:11
par busard_des_roseaux » 23 Juil 2008, 15:11
Bjr,
trois petites idées sans avoir la solution:
1) on peut sortir
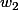
de l'intégrale par
 dt = \Im( \int e^{it}dt ) =)
2) en utilisant les parités et les périodes, se ramener à un intervalle
plus court où
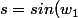)
est bijectif, croissant
on doit pouvoir se ramener à une intégrande du style

3) sinon, si on développe en série le sinus (extérieur), on récupère des intégrales de Wallis (d'intégrandes des puissances du sinus intérieur.)
 par busard_des_roseaux » 23 Juil 2008, 15:49
par busard_des_roseaux » 23 Juil 2008, 15:49
bon, en fait , il semble que ce soient les idées (1) et (3) qui marchent:
- on sort w2 de l'intégrale
- on considère le sinus comme la partie imaginaire de l'exponentielle
- on développe en série
- on tombe, après réduction à l'intervalle
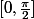
,
sur des intégrales de Wallis que l'on calcule.
Les termes d'exposants impairs ont déja disparu.
- ça se simplifie. Tu devrais obtenir le résultat sous forme d'une jolie série qui "ressemble" à l'exponentielle. Il ne reste ensuite plus qu'à séparer partie réelle et imaginaire.
-
chwebij
- Messages: 5
- Enregistré le: 23 Juil 2008, 14:37
-
 par chwebij » 23 Juil 2008, 16:41
par chwebij » 23 Juil 2008, 16:41
 par busard_des_roseaux » 23 Juil 2008, 17:04
par busard_des_roseaux » 23 Juil 2008, 17:04
super.
sinon les intégrales de polynomes sur [-1,1] avec le poids

ont une quadrature exacte avec une formule
liée aux polynomes de Tchebycheff dûe à Gauss.
Je t'écris ça à tout hasard, si jamais tu en as besoin.
Pour les résidus, j'y crois pas trop.
-
chwebij
- Messages: 5
- Enregistré le: 23 Juil 2008, 14:37
-
 par chwebij » 23 Juil 2008, 17:11
par chwebij » 23 Juil 2008, 17:11
mouef... de plus ce résultat ne m'arrange pas du tout car unitilisable..j'aurais voulu garder juste les premiers termes de la série (pour du numérique) mais vu que
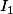
est extrement grand (de l'orde de 10^12), les termes de la série doivent décroitre à partir d'un n assez grand.
sinon encore une fois merci
 par busard_des_roseaux » 23 Juil 2008, 17:20
par busard_des_roseaux » 23 Juil 2008, 17:20
chwebij a écrit:mouef... de plus ce résultat ne m'arrange pas du tout car unitilisable..j'aurais voulu garder juste les premiers termes de la série (pour du numérique) mais vu que
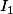
est extrement grand (de l'orde de 10^12), les termes de la série doivent décroitre à partir d'un n assez grand.
sinon encore une fois merci
euh, oui et non.
La série trouvée, elle ressemble quand même (très vaguement) à celle de

, c'est-à dire, bien qu'ayant perdu les propriétés très particulières de la série exponentielle, on peut quand même travailler avec cette série, en termes de limite, de dérivée, d'équivalent,
de comportement asymptotique,etc..
en particulier, elle doit tendre vers zéro très vite quand
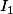
tend vers

-
JJa
- Membre Relatif
- Messages: 254
- Enregistré le: 06 Mar 2008, 15:52
-
 par JJa » 23 Juil 2008, 21:33
par JJa » 23 Juil 2008, 21:33
Bonjour chwebij,
c'est une fonction de Bessel J0(x)
Tu dois trouver = -sin(w)*J0(x) avec x=rac(2*I)
-
chwebij
- Messages: 5
- Enregistré le: 23 Juil 2008, 14:37
-
 par chwebij » 24 Juil 2008, 09:20
par chwebij » 24 Juil 2008, 09:20
aaaaaaaaaah
je savais bien que Bessel y était pour quelque chose!!!
franchement je voudrais vous dire un grand bravo car ca me permettra d'aller plus loin dans mon stage!!!Encore merci!!
-
chwebij
- Messages: 5
- Enregistré le: 23 Juil 2008, 14:37
-
 par chwebij » 25 Juil 2008, 09:13
par chwebij » 25 Juil 2008, 09:13
bonjour
en fait j'ai trouver dans un bouquin, la formule:
+a)=\sum_n sin(n*b+a) J_n(u))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
