bjr,
je connaissais pas cette théorie qui s'appelle "propriétés métriques des nappes" , par exemple dans le Tauvel , géométrie pour l'agreg.
Une surface résulte d'un paramètrage à deux variables:
 \rightarrow X(u,v) \in \mathbb{R^3})
X est un vecteur de
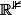
de coordonnées
,y(u,v),z(u,v)))
au moins localement.
Avec tes notations:
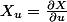
c'est bien ça ?
Toujours avec les notations, il semble qu'on étudie un arc paramétré
sur la surface
,v(t)))
?
Il me semble qu'il faut alors redériver , par rapport à t, le vecteur:
)
pour obtenir une dérivée seconde. Ce qui donne, sur la 1ère coordonnée:
 + v' \left( \frac{\partial^2 x}{\partial v \partial u} u' + \frac{\partial^2 x}{\partial v^2} v' \right) + v{' '} \frac{\partial x}{\partial v})
même méthode pour les deux autres coordonnées.
Dans un tout autre ordre d'idée,
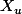
et

est supposée une famille libre du plan vectoriel tangent. On définit alors une forme quadratique sur ce plan vectoriel tangent, dite "seconde forme fondamentale" et que les coeff de cette forme s'expriment agréablement si l'équation de la surface a été rendue cartésienne, via le théorème des fonctions implicites,
de la forme
=X_0+ u \vec{i}+v \vec{j}+\phi(u,v) \vec{k})

données par le théorème des fonctions implicites.
? :doh: