Formules usuelles des dérivées et dérivées n-ième
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 05 Sep 2006, 12:12
par haydenstrauss » 05 Sep 2006, 12:12
et dans le lien que tu as donné il n'y a que les dérivées premieres.
y'a des dérivé avec de spuissance n
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 05 Sep 2006, 12:14
par nox » 05 Sep 2006, 12:14
oui mais c'est pas ca qu'il voulait il voulait les dérivées n-iemes
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 05 Sep 2006, 12:22
par tize » 05 Sep 2006, 12:22
nox a écrit:apparemment...mais uniquement dans ce cas particulier parce que
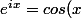 - i (cos(x))')
Mille excuses, c'est ma faute, je débarque et je lis pas, j'ai cru que c'était des puissances.
Au temps pour moi. :marteau:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 05 Sep 2006, 12:29
par nekros » 05 Sep 2006, 12:29
tize a écrit:Mille excuses, c'est ma faute, je débarque et je lis pas, j'ai cru que c'était des puissances.
Au temps pour moi. :marteau:
Aucun problème tize :happy3:
Mais tu m'as fait peur :ptdr: parce que je ne voyais pas du tout mon erreur.
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 05 Sep 2006, 12:32
par nox » 05 Sep 2006, 12:32
tize a écrit:Mille excuses, c'est ma faute, je débarque et je lis pas, j'ai cru que c'était des puissances.
Au temps pour moi. :marteau:
forcément avec les puissances ca marche moins bien :ptdr:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 05 Sep 2006, 19:55
par nada-top » 05 Sep 2006, 19:55
Re,
merci Nekros pour ton indice de lineariser
)
:we:
voilà ce que je trouve :
)^{(n)} = (\frac{1}{2} - \frac{1}{2}cos(2x))^{(n)} = -\frac{1}{2}(cos(2x))^{(n)} <br /> = -\frac{1}{2}Re(e^{i2x})^{(n)}<br /> = -\frac{1}{2}.2^n Re(i^n.e^{i2x}) = -2^{n-1} Re(e^{i(2x+\frac{n\pi}{2})}) <br />= 2^{n-1} cos(2x+(n-1)\frac{\pi}{2} - \frac{\pi}{2} ) = 2^{n-1} . sin(2x + (n-1)\frac{\pi}{2} ).)
c bon?
Ps : j'ai essayé de t'envoyer la soluce par mp mais ta messagerie est pleine .
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 05 Sep 2006, 20:09
par nekros » 05 Sep 2006, 20:09
salut,
Pour la dérivée nième de
)
, je trouve
)
PS : pour la messagerie, c'est réglé :lol4:
-
JustineH
- Messages: 1
- Enregistré le: 27 Fév 2020, 14:45
-
 par JustineH » 27 Fév 2020, 15:04
par JustineH » 27 Fév 2020, 15:04
Si j'ai bien compris ce que tu demandes, la dérivée n-ième de sin(x) est sin( x + n * pi/2) et la dérivée n-ième de cos(x) est cos( x + n * pi/2).
En effet, en prenant l'exemple de sin(x) dérivé n fois:
- dérivée première de sin(x) = cos(x) = sin(x+pi/2) [formules de trigonométrie]
- dérivée seconde de sin(x) = dérivée première de cos(x) = -sin(x) = sin( x + pi) = sin ( x + 2*pi/2)
- dérivée troisième de sin(x) = dérivée première de -sin(x) = -cos(x) = -sin( x + pi/2) .
En posant y = x + pi/2, tu obtiens sin( y + pi ) = -sin(y) = -sin(x + pi/2).
Ainsi, la dérivée troisième de sin(x) est sin( y + pi) = sin( x + pi/2 + pi ) = sin (x + 3*pi/2).
Etc, jusqu'a en déduire la formule générale de la dérivée n-ième que tu peux vérifier par récurrence.
Voila, j'espère que j'ai pu t'aider, j'ai essayé d'être le plus précise possible en te donnant la démonstration
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 27 Fév 2020, 18:00
par GaBuZoMeu » 27 Fév 2020, 18:00

J'espère que depuis 13-14 ans, la personne qui se posait des questions est passée à autre chose.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
 J'espère que depuis 13-14 ans, la personne qui se posait des questions est passée à autre chose.
J'espère que depuis 13-14 ans, la personne qui se posait des questions est passée à autre chose.