Une histoire d'e.v.n

par **road runner** » 22 Fév 2008, 19:22

bonsoir a tous
si on a (E,||.||) un e.v.n sur R et f une forme lineaire de E dans R et en posant

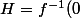je voudrais montrer que si E est différent de l'adhérence de H alors H est un fermé, et je vois pas trop comment faire.
un peu d'aide ?

merci d'avance

par **ffpower** » 22 Fév 2008, 20:09

c faux,c vrai que si f est continue,sinon H est dense

par **kazeriahm** » 22 Fév 2008, 20:10

salut

H est un sev de E (c'est Ker f) il est soit dense soit fermé dans E...

par **kazeriahm** » 22 Fév 2008, 20:10

ffpower a écrit:c faux,c vrai que si f est continue,sinon H est dense

bah jutement H n'est pas dense...

par **road runner** » 22 Fév 2008, 20:12

c'est donné que E est différent de l'adherence de H

par **yos** » 22 Fév 2008, 21:01

mais

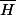
est un sev et H est un hyperplan donc

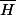
est égal à H ou à E.

par **klaus2008** » 22 Fév 2008, 21:29

bonsoir à tous
yos tu as dit adhérence de H est un Hyperplan , qqn m'explique un peu...

par **ThSQ** » 22 Fév 2008, 21:34

klaus2008 a écrit:bonsoir à tous
yos tu as dit adhérence de H est un Hyperplan , qqn m'explique un peu...

Non il a dit que c'était un sev (l'adhérence d'un sev = un sev, exo : dans quel cas l'intérieur est-il aussi un sev ?).

Donc l'adhérence de H est ou bien H (s'il est fermé) ou bien E sinon.

par **kazeriahm** » 22 Fév 2008, 21:42

c'est vrai qu'ici H est un hyperplan (c'est le noyau d'une forme lineaire : il existe un espace de dimension 1 D tel que D est le supplementaire de H dans E) donc c'est plus simple

par **ffpower** » 22 Fév 2008, 21:46

pardon j avais mal lu lol

par **road runner** » 22 Fév 2008, 21:48

est ce que vous pouvez m'exliquer pourquoi l'adherence de H est egale soit à H ou à E ,merci

par **ThSQ** » 22 Fév 2008, 21:53

road runner a écrit:est ce que vous pouvez m'exliquer pourquoi l'adherence de H est egale soit à H ou à E ,merci

Entre un hyperplan et l'espace complet y'a pas beaucoup de place pour caser un sev ...

par **yos** » 22 Fév 2008, 23:29

ThSQ a écrit:exo : dans quel cas l'intérieur est-il aussi un sev

Que si le sev est E? Sinon l'intérieur est assez vide.

par **ThSQ** » 22 Fév 2008, 23:55

yos a écrit:Que si le sev est E? Sinon l'intérieur est assez vide.

:++: (mais trop facile pour toi yos !)

par **busard_des_roseaux** » 23 Fév 2008, 01:01

ThSQ a écrit:Non il a dit que c'était un sev (l'adhérence d'un sev = un sev, exo : dans quel cas l'intérieur est-il aussi un sev ?).

Si l'intérieur d'un s.e.v est un espace vectoriel , il contient une boule

, par symétrie une boule

avec la demi-somme une boule

et par homothétie l'espace vectoriel tout entier.

par **ThSQ** » 23 Fév 2008, 16:14

Une tentative de "généralisation" (une mauvaise manie chez moi ...) avec un angle d'attaque différent :

A une algèbre de Banach (commutative pour simplifier).

* J un idéal de A. J est-il nécessairement fermé ?
* Quid si J est maximal ?

Enjoy.

Une histoire d'e.v.n

une histoire d'e.v.n

Qui est en ligne