Salut à tous,
Doraki a écrit:On peut supposer que f(a)=f(b)=0 quitte à ajouter une fonction affine.
Il faut alors montrer que f est nulle.
C'est pas très très dur par l'absurde (pardonne-moi, leon).
Faut néanmoins utiliser la propriété que toute partie non vide de R a une borne inférieure.
Arf... l'absurde... :ptdr:
Bon, de manière directe, c'est simple, en utilisant la densité des fractions

(z,n entiers) dans R. Comment se fait-il que personne n'y pense ?...
Notons (D) la droite passant par les points
))
et
))
.
Pour un réel t compris entre 0 et 1, on note P(t) le point
))
où
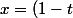a + tb)
(barycentre de a et b)
Alors l'hypothèse dit que
P(1/2) est sur (D),
puis P(1/4) , P(3/4) sont sur (D),
puis P(1/8) , P(3/8) , P(5/8), P(7/8) sont sur (D),
...bref tous les points
)
sont alignés sur (D)
Enfin la continuité de f et la densité des fractions

permettent de conclure que tous les P(t) sont alignés sur (D).
Non ?
(j'aurais pu poser a=0 et b=1 pour que les notations soient plus simples.)
