Relations binaires-Equivalence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
zinedine
- Membre Naturel
- Messages: 21
- Enregistré le: 15 Nov 2007, 23:52
-
 par zinedine » 17 Jan 2008, 17:08
par zinedine » 17 Jan 2008, 17:08
bonjour ,
j ai un petit problème de comprehension au niveau des relations binaires.
soit E = N * N , on définit R par (a,b) R (a',b') <==> a+b' = b +a'
1-Montrer que R est une relation d' equivalence
2-identifier E/R
Pour la 1 je dois demontrer que la relation est reflexive , symetrique et transitive.
mais je ne vois helas pas comment faire , comment me le representer
en fait je ne comprends pas grand chose , un petit coup de main serait le bienvenue
Merci
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 17 Jan 2008, 17:13
par Babe » 17 Jan 2008, 17:13
zinedine a écrit:bonjour ,
j ai un petit problème de comprehension au niveau des relations binaires.
soit E = N * N , on définit R par (a,b) R (a',b') a+b' = b +a'
1-Montrer que R est une relation d' equivalence
2-identifier E/R
Pour la 1 je dois demontrer que la relation est reflexive , symetrique et transitive.
mais je ne vois helas pas comment faire , comment me le representer
en fait je ne comprends pas grand chose , un petit coup de main serait le bienvenue
Merci
utilise simplement les definition d'une relation d'equivalence (reflexive, sym, trans) et c'est immediat
-
zinedine
- Membre Naturel
- Messages: 21
- Enregistré le: 15 Nov 2007, 23:52
-
 par zinedine » 17 Jan 2008, 21:45
par zinedine » 17 Jan 2008, 21:45
bonjour,
merci pour ta réponse mais c est une chose que je n arrive pas a faire , peux tu seulement me donner la demarche a suivre?
comment dessiner la graphe de la relation , je ne comprends pas trop , ici on parle de couple d éléments et non d' un seul élément c est ce qui me pose probleme.
merci
-
seriousme
- Membre Relatif
- Messages: 122
- Enregistré le: 26 Fév 2007, 13:10
-
 par seriousme » 17 Jan 2008, 23:06
par seriousme » 17 Jan 2008, 23:06
Réfléxivité :
il faut montrer que :
 R (a, b))
.
 R (a, b) \Longleftrightarrow a + b = a +b)
Or
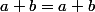
est vrai pour tout
 \in \mathbb{N}^2)
.
Donc la relation R est réfléxive .
Transitivité :
il faut montrer le prédicat :
 \in \mathbb{N}^6,\ (a, b) R (c, d) \wedge (c, d) R (e, f) \Longrightarrow (a, b) R (e, f))
.
 R (c, d) \Longleftrightarrow a + d = b + c)
 R (e, f) \Longleftrightarrow c + f = d + e)
en additionnant :
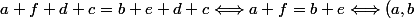 R (e, f))
.
Donc la relation est transitive .
...
-
zinedine
- Membre Naturel
- Messages: 21
- Enregistré le: 15 Nov 2007, 23:52
-
 par zinedine » 26 Jan 2008, 01:31
par zinedine » 26 Jan 2008, 01:31
Ok merci je comprends mieux , mais quels sont les classes d equivalence ??? :triste:
merci
-
bruce.ml
- Membre Rationnel
- Messages: 630
- Enregistré le: 18 Juin 2007, 23:54
-
 par bruce.ml » 26 Jan 2008, 01:50
par bruce.ml » 26 Jan 2008, 01:50
zinedine a écrit:Ok merci je comprends mieux , mais quels sont les classes d equivalence ??? :triste:
merci
Salut,
prends un point (a,b) de E, et demande toi quels sont tous les points qui sont en relation avec lui


-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 26 Jan 2008, 14:16
par leon1789 » 26 Jan 2008, 14:16
Hors sujet : pour un exercice sur les relations d'équivalence, c'est "nul"... Que peut-on comprendre avec ce genre d'exo où il n'y a rien à démontrer ? Et en plus, il n'y a qu'une seule classe... vraiment super comme exemple de relation d'équivalence !
Désolé :stupid_in je sors...
-
zinedine
- Membre Naturel
- Messages: 21
- Enregistré le: 15 Nov 2007, 23:52
-
 par zinedine » 27 Jan 2008, 00:24
par zinedine » 27 Jan 2008, 00:24
salut ,
ce qui me pose probleme c est que l 'on parle de couple {a,b} et {a',b'} ,le premier couple {a,b} apparatient au premier ensemble N et le deuxieme au deuwieme ensemble N.
Est ce bien ça?
merci
-
bruce.ml
- Membre Rationnel
- Messages: 630
- Enregistré le: 18 Juin 2007, 23:54
-
 par bruce.ml » 27 Jan 2008, 11:39
par bruce.ml » 27 Jan 2008, 11:39
non, un couple (a,b) appartient à E. c'est un couple de nombres entiers. et tous les couples appartiennent au même ensemble E.
-
zinedine
- Membre Naturel
- Messages: 21
- Enregistré le: 15 Nov 2007, 23:52
-
 par zinedine » 01 Fév 2008, 23:37
par zinedine » 01 Fév 2008, 23:37
salut ,
alors (a,b) n est pas un couple mais un élément de E , en ce qui concerne les classes d equivalence , pour moi ca me parait moins évident.
J avais trouvé je ne sais plus comment que l ensemble des classes d equivalences formé l ensemble Z : les entiers relatifs .
merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
