Intégration par partie?
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
tlzl
- Membre Naturel
- Messages: 51
- Enregistré le: 03 Nov 2007, 14:43
-
 par tlzl » 16 Jan 2008, 13:16
par tlzl » 16 Jan 2008, 13:16
Bonjour,
Je n'arrive pas à résoudre
intégrale 0 à 2 de x exp(3x)
vu qu'il y un produit j'opterai pour l'intégration par partie mais je n'arrive pas bien manipuler ce théorème, pourriez-vous me donner le dvp pour que je comprenne une fos pour toute?
Merci d'avance
-
sylar44
- Messages: 7
- Enregistré le: 16 Jan 2008, 13:28
-
 par sylar44 » 16 Jan 2008, 13:34
par sylar44 » 16 Jan 2008, 13:34
tu as x*exp(3x)
donc oui tu fais une integration par partie
la formule est : F=[u*v] - int(u'*v') entre 0 et 2.
tu devrais voir que si tu derive l'exponentiel pour avoir [u'*v] tu vas tourner en rond.
donc tu prends u(x)=x
et v(x)=exp(3x)
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 16 Jan 2008, 13:37
par gol_di_grosso » 16 Jan 2008, 13:37
dans ton cours :

là il faut virer ce x devant l'exp
donc on pose u=x et v' =exp(3x)
-
Antho07
- Membre Rationnel
- Messages: 741
- Enregistré le: 26 Oct 2007, 19:12
-
 par Antho07 » 16 Jan 2008, 13:44
par Antho07 » 16 Jan 2008, 13:44
deja, essayons de comprendre d'ou vient la formule de l'integration par partie.
on sait dériver un produit de fonction.
 \times v(x))'=u'(x)\times v(x) + u(x) \times v'(x))
on obtient alors facilement:
 \times v'(x)=(u(x) \times v(x))' - u'(x) \times v(x))
maintenant integrons:
 \times v'(x) dx=\int_{a}^{b} ((u(x) \times v(x))' - u'(x) \times v(x))dx)
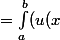 \times v(x))' dx - \int_{a}^{b} (u'(x) \times v(x))dx.)
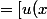 \times v(x)]_{a}^{b} - \int_{a}^{b} u'(x) \times v(x) dx)
Résumons:
 \times v'(x) dx =[u(x) \times v(x)]_{a}^{b} - \int_{a}^{b} u'(x) \times v(x)dx)
.
ici, posons alors.
u(x)=x
v'(x)=exp(3x).
-
tlzl
- Membre Naturel
- Messages: 51
- Enregistré le: 03 Nov 2007, 14:43
-
 par tlzl » 16 Jan 2008, 13:51
par tlzl » 16 Jan 2008, 13:51
F= (1*exp(3x))- int (x*3exp(3x))
F=(1*exp(3x))- ( 1/2 x^2 * 1/3exp(3x)
c'est juste?
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 16 Jan 2008, 13:53
par gol_di_grosso » 16 Jan 2008, 13:53
bon
u(x)=x
v'(x)=exp(3x)
donne nous u'(x) et v(x)
-
tlzl
- Membre Naturel
- Messages: 51
- Enregistré le: 03 Nov 2007, 14:43
-
 par tlzl » 16 Jan 2008, 14:01
par tlzl » 16 Jan 2008, 14:01
merci de vos réponses
= x*1/3 exp(3x) - int 1*1/3 exp(3x)
= x*1/3 exp(3x) - 1/3 int exp(3x)
= x*1/3 exp(3x) - 1/3 + 1/3 exp(3x) le tout intégré entre 0 et 2
c'est ok ?
-
gol_di_grosso
- Membre Irrationnel
- Messages: 1402
- Enregistré le: 22 Sep 2007, 11:28
-
 par gol_di_grosso » 16 Jan 2008, 14:06
par gol_di_grosso » 16 Jan 2008, 14:06
=(1/9) \exp(3x))
et puis fini ton intégration entre 0 et 2
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
