J'ai plusieurs questions concernant les intégrales :
Les intégrales multiples, je crois bien que ça s'associe à des fonctions à plusieurs variables. Or si j'ai bien compris le principe, il s'agit simplement de transformer une intégrale multiple en plusieurs (une somme peut être ???) intégrale simple, tout comme la dérivation à plusieurs variables se ramène simplement à la dérivation simple à une variable grâce aux dérivées partielles. Ma question est assez simple, outre le fait que je vous demande de me corriger là où je dis une connerie, pouvez vous m'expliquer simplement (en ayant en tête qu'on est dans la section lycée...) comment calculer une intégrale multiple et si possible me donner une formule ultra généraliste résumant pour une fonction à n variables...
La deuxième question, concerne l'expression '' intégrer '' une équation diff. Tout le monde sait que l'intégration est l'opération contraire de la dérivation. À ce titre je me posais la question de savoir si lorsqu'on passer d'une équation diff. à une équation algébrique usuelle (raisonnement souvent utilisé par ailleurs comme j'ai pu le voir en physique (c'est tellement plus simple de poser des équations diff grâce aux principes de conservations...) pour des petites formules de mécanique ou de thermodynamique...), on transformer chaque membre en lui appliquant une opération (l'intégration dans ce cas là), déjà j'aurais voulu savoir si les bornes de l'intégrale pouvait être pris au hasard ou en toute généralité et si ils étaient les mêmes pour les deux membres (ça ne me paraît pas trivial), d'ailleurs je n'ai pas souvent vu les intégrales écrites explicitement (sûrement parce que dérivation + intégration = fonction de départ, c'est trivial et les auteurs l'omettent ??).
Ma troisième et dernière question concerne le théorème d'intégration par parties, il a été enlevé du programme de lycée, quel dommage je ne vous le fait pas dire... J'en suis réduit à regarder sur des bouquins d'exos plus anciens et là je tombe souvent sur des énoncés du type : '' après plusieurs intégrations par parties successives, vous déterminerez que... '', or, j'ai beau regarder la formule d'intégration par parties dans le bout des yeux, je ne vois pas comment on peut simplifier une intégrale en la remplaçant par une autre intégrale ? :o Y'a peut être une astuce, mais sur le coup je ne la voit pas, et comme on a pas vu ça en cours...
Merci pour votre aide !
Intégrale et Intégration par partie
4 messages
- Page 1 sur 1
par Robic » 10 Juin 2014, 20:45
Ah, tu te poses des questions un peu en avance !
Il y a deux cas :
1) Dans la fonction à intégrer, on peut séparer les variables. Alors on pourra remplacer l'intégrale double par un produit d'intégrales simples.
Exemple très connu :
}\, dx\, dy = \int\int_{[0,a]\times [0,a]} e^{-x^2}e^{-y^2}\, dx\, dy = \int_0^a e^{-x^2}\, dx \int_0^a e^{-y^2}\, dy = I^2)
où
(En fait, le but est de calculer I, donc la fonction à intégrer n'a pas de primitive exprimable sous forme de fonctions usuelles, en se ramenant à une intégrale double qui, à l'aide d'un changement de variable en coordonnées polaires, sera calculable. C'est une astuce célèbre.)
2) Mais dans le cas général on ne peut pas séparer les deux variables.
Exemple idiot (où A est un ensemble inclus dans le demi-plan x+y > 0) :
 \, dx \, dy.)
Là je ne crois pas qu'il y ait une méthode générale.
Concernant la deuxième question, je n'ai pas compris, mais j'ai lu rapidement. Quelqu'un viendra sûrement l'aborder.
Et pourtant... Regarde des exercices de base et leur correction.
Exemple classique (où a et b sont >0) :
 \,dx = \int_a^b 1 \cdot \ln(x) \,dx)
(grosse astuce : on multiplie par 1...)
On pose :
u'(x) = 1, donc u(x) = x,
 = \ln(x))
, donc  = \frac{1}{x}.)
Du coup :
 \,dx = \left\[ x\ln(x) \right\]_a^b - \int_a^b x \cdot \frac{1}{x} \, dx,)
etc.
comment calculer une intégrale multiple et si possible me donner une formule ultra généraliste résumant pour une fonction à n variables...
Il y a deux cas :
1) Dans la fonction à intégrer, on peut séparer les variables. Alors on pourra remplacer l'intégrale double par un produit d'intégrales simples.
Exemple très connu :
où
(En fait, le but est de calculer I, donc la fonction à intégrer n'a pas de primitive exprimable sous forme de fonctions usuelles, en se ramenant à une intégrale double qui, à l'aide d'un changement de variable en coordonnées polaires, sera calculable. C'est une astuce célèbre.)
2) Mais dans le cas général on ne peut pas séparer les deux variables.
Exemple idiot (où A est un ensemble inclus dans le demi-plan x+y > 0) :
Là je ne crois pas qu'il y ait une méthode générale.
Concernant la deuxième question, je n'ai pas compris, mais j'ai lu rapidement. Quelqu'un viendra sûrement l'aborder.
or, j'ai beau regarder la formule d'intégration par parties dans le bout des yeux, je ne vois pas comment on peut simplifier une intégrale en la remplaçant par une autre intégrale ?
Et pourtant... Regarde des exercices de base et leur correction.
Exemple classique (où a et b sont >0) :
On pose :
u'(x) = 1, donc u(x) = x,
Du coup :
par capitaine nuggets » 10 Juin 2014, 21:19
Salut !
- Pour calculer des intégrales multiple, on peut effectuer des changement de variable polaire, cylindrique, sphérique, affine etc... (par exemple, pour redémontrer l'aire d'un cylindre, d'une sphère etc...).
- Lorsque la fonction en question admet certaines propriétés comme par exemple être un polynôme d'inconnues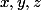
(=x^3y+2x^2y^2z^2+x-y)
), calculer l'intégrale multiple de \ dxdydz)
revient à calculer successivement les intégrales de )
par rapport à 
, puis 
puis 
(par exemple) :
\ dxdydz=\iint\left( \int P(x,y,z)\ dx\right) dydz=\cdots)
.
Quand tu intègres par rapport à une variable, les autres se comporte comme des constantes.
- Si une fonction
s'écrit sous la forme = \prod_{k=1}^n f_k(x_k))
alors on a \ dx_1dx_2...dx_n = \prod_{k=1}^n \left( \int f_k(x_k)\ dx_k\right))
Le problème en physique, c'est qu'on utilise souvent de puissants objets mathématiques sans vraiment grande rigueur... En particulier, on intègres des fonctions sur un domaine pas toujours très bien clair, les fonctions ne sont peut-être pas continues, etc...
L'intégration par partie peut servir par exmeple à calculer des intégrales de fonctionse^x)
, \sin(x))
, etc...
Par exemple, si je ne dis pas de bêtises, si=n,n\ge 1)
, alors il faut effectuer 
intégration par parties pour calculer une intégrale de .
AK-47 a écrit:J'ai plusieurs questions concernant les intégrales :
Les intégrales multiples, je crois bien que ça s'associe à des fonctions à plusieurs variables. Or si j'ai bien compris le principe, il s'agit simplement de transformer une intégrale multiple en plusieurs (une somme peut être ???) intégrale simple, tout comme la dérivation à plusieurs variables se ramène simplement à la dérivation simple à une variable grâce aux dérivées partielles. Ma question est assez simple, outre le fait que je vous demande de me corriger là où je dis une connerie, pouvez vous m'expliquer simplement (en ayant en tête qu'on est dans la section lycée...) comment calculer une intégrale multiple et si possible me donner une formule ultra généraliste résumant pour une fonction à n variables...
- Pour calculer des intégrales multiple, on peut effectuer des changement de variable polaire, cylindrique, sphérique, affine etc... (par exemple, pour redémontrer l'aire d'un cylindre, d'une sphère etc...).
- Lorsque la fonction en question admet certaines propriétés comme par exemple être un polynôme d'inconnues
Quand tu intègres par rapport à une variable, les autres se comporte comme des constantes.
- Si une fonction
AK-47 a écrit:
La deuxième question, concerne l'expression '' intégrer '' une équation diff. Tout le monde sait que l'intégration est l'opération contraire de la dérivation. À ce titre je me posais la question de savoir si lorsqu'on passer d'une équation diff. à une équation algébrique usuelle (raisonnement souvent utilisé par ailleurs comme j'ai pu le voir en physique (c'est tellement plus simple de poser des équations diff grâce aux principes de conservations...) pour des petites formules de mécanique ou de thermodynamique...), on transformer chaque membre en lui appliquant une opération (l'intégration dans ce cas là), déjà j'aurais voulu savoir si les bornes de l'intégrale pouvait être pris au hasard ou en toute généralité et si ils étaient les mêmes pour les deux membres (ça ne me paraît pas trivial), d'ailleurs je n'ai pas souvent vu les intégrales écrites explicitement (sûrement parce que dérivation + intégration = fonction de départ, c'est trivial et les auteurs l'omettent ??).
Le problème en physique, c'est qu'on utilise souvent de puissants objets mathématiques sans vraiment grande rigueur... En particulier, on intègres des fonctions sur un domaine pas toujours très bien clair, les fonctions ne sont peut-être pas continues, etc...
AK-47 a écrit:Ma troisième et dernière question concerne le théorème d'intégration par parties, il a été enlevé du programme de lycée, quel dommage je ne vous le fait pas dire... J'en suis réduit à regarder sur des bouquins d'exos plus anciens et là je tombe souvent sur des énoncés du type : '' après plusieurs intégrations par parties successives, vous déterminerez que... '', or, j'ai beau regarder la formule d'intégration par parties dans le bout des yeux, je ne vois pas comment on peut simplifier une intégrale en la remplaçant par une autre intégrale ?Y'a peut être une astuce, mais sur le coup je ne la voit pas, et comme on a pas vu ça en cours...
Merci pour votre aide !
L'intégration par partie peut servir par exmeple à calculer des intégrales de fonctions
Par exemple, si je ne dis pas de bêtises, si
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
par paquito » 11 Juin 2014, 10:20
Un exposé complet sur les intégrales multiples prendrait un nombre de pages considérables. Déjà on intègre sur une partie de R² et il arrive, s'il on a des variables indépendantes à se ramener à un produit d'intégrales comme te le montres robic; mais si les variables sont dépendantes, il faut savoir dans quel ensemble évolue par exemple y pour x fixé; on a aussi des théorèmes qui permettent de permuter les intégrales (FUBINI); mais là tu abordes un sujet trop vaste pour être expliquer rapidement. il faut y allar progressivement et pas mal manipuler; tu as tout le temps...
Pour ta 2° question, lorsque l'on recherche une primitive, on dit que l'on intègre, ou parfois que l'on fait une quadrature; pour les équations différentielles, plusieurs types (à variables séparables) se résolvent par une intégrale et donc je pense que le terme intégrer s'est imposé à la place de résoudre.
Pour l'intégration par parties,c'est très rusé!
On a
donc on remplace le calcul qu'on na sait pas faire de
par le calcul d'une autre intégrale
que l'on peut savoir résoudre et en mathématiques, l'intégration par parties est très utilisée et pas seulement pour calculer une intégrale.
Je de donne un exemple quand même, mais il y a un résultat que j'utilise qui est difficile de démontrer.
La définition officielle de'l'aire d'un cercle de rayon centré en 0 est:
. On passe aux coordonnées polaires
)
comme en complexe, mais il faut remplacer dxdy par 
, ce qui donne:
d\theta)
=
Je passe en polaire pour avoir des variables indépendantes, mais cela m'oblige à remplacer dxdy par
étant le jacobien de la transformation.
Comme tu vois, il te reste plein de choses intéressantes à voir.
Pour ta 2° question, lorsque l'on recherche une primitive, on dit que l'on intègre, ou parfois que l'on fait une quadrature; pour les équations différentielles, plusieurs types (à variables séparables) se résolvent par une intégrale et donc je pense que le terme intégrer s'est imposé à la place de résoudre.
Pour l'intégration par parties,c'est très rusé!
On a
Je de donne un exemple quand même, mais il y a un résultat que j'utilise qui est difficile de démontrer.
La définition officielle de'l'aire d'un cercle de rayon centré en 0 est:
Je passe en polaire pour avoir des variables indépendantes, mais cela m'oblige à remplacer dxdy par
Comme tu vois, il te reste plein de choses intéressantes à voir.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :