Problème factorisation..
22 messages
- Page 1 sur 2 - 1, 2
Problème factorisation..
Bonjour.
Je bloque sur un exercice de factorisation.J'ai fait l'exercice en entier SAUF ces 2 calculs que je n'arrive pas.Donc je ne vous demande pas de me faire l'exercice mais de me donner le début des calculs ainsi qu'une explication sur la méthode à utiliser pour factoriser les calculs de ce type.Les voila:
1. (x-2)(x+4)-(x-2)
= ?
2. x²-2/3x+1/9
= ?
Voila merci d'avance.
Celui-ci me bloque également car la racine carré de 12 est un nombre décimal,ce qui me bloque:
12x²-24x+12
Je bloque sur un exercice de factorisation.J'ai fait l'exercice en entier SAUF ces 2 calculs que je n'arrive pas.Donc je ne vous demande pas de me faire l'exercice mais de me donner le début des calculs ainsi qu'une explication sur la méthode à utiliser pour factoriser les calculs de ce type.Les voila:
1. (x-2)(x+4)-(x-2)
= ?
2. x²-2/3x+1/9
= ?
Voila merci d'avance.
Celui-ci me bloque également car la racine carré de 12 est un nombre décimal,ce qui me bloque:
12x²-24x+12
Bonjour;
^2) sénonce :
sénonce :
) au carré est égal au carré du premier terme
au carré est égal au carré du premier terme  ; plus deux fois le premier multiplié par le second ;
; plus deux fois le premier multiplié par le second ; 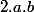 , plus le carré du second
, plus le carré du second 
le jeu consiste à voir le dèbut dun carré dans lexpression
(\frac{1}{3})x)
une fois que lon n en est là; on peut penser que lexpression correspond au début de
^2) en effet si lon développe
en effet si lon développe  -2fois le premier terme x par le second
-2fois le premier terme x par le second  plus le carré du second
plus le carré du second ^2)
finalement on obtient

une autre façon :
^2 = a^2 x^2 + 2axb + b^2 = a^2 x^2 + 2abx + b^2)
ce qui resemble un peu à notre expression de départ
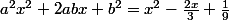 si lon compare les termes de droite et de gauche
si lon compare les termes de droite et de gauche
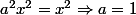
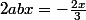
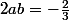
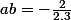 et comme
et comme 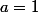
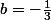 doù en
doù en
remplaçant et
et dans
dans ^2)
^2=(x-\frac{1}{3})^2=x^2 - \frac{{2x}}{3} + \frac{1}{9})
un autre exemple
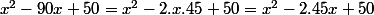
on voit le second terme qui doit-être 45
^2=x^2-45.2.x+45^2)
mais cette expression diffèrre de 45^2 par rapport à lexpression de départ
donc pour garder légalité on fait :
^2-45^2)+50=(x-45)^2-2025+50=(x-45)^2-1975=A^2-B^2)
cest de la forme(A+B)) avec
avec 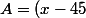) ;
; 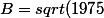)
doù-sqrt(1975)((x-45)+sqrt(1975)))
on a bien^2-1975=x^2-90x+45^2-1975=x^2-90x+2025-1975=x^2-90x+50)
le jeu consiste à voir le dèbut dun carré dans lexpression
une fois que lon n en est là; on peut penser que lexpression correspond au début de
finalement on obtient
une autre façon :
ce qui resemble un peu à notre expression de départ
remplaçant
un autre exemple
on voit le second terme qui doit-être 45
mais cette expression diffèrre de 45^2 par rapport à lexpression de départ
donc pour garder légalité on fait :
cest de la forme
doù
on a bien
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
