Triangle d'aire minimale

[Tagogo]

Salut ! je suis en 1°S, j'ai un exercice à faire :
soit A (1;2). à chaque point P de l'axe (Ox) d'abscisse x (x>1), on associe le point Q de l'axe (Oy) de façon que A, P et Q soient alignés. On désigne S(x) l'aire du triangle OPQ.

1) à l'aide d'un logitiel de géométrie dynamique, simuler la situation décrite ci-dessus.
Ca c'est bon, je l'ai fait avec "Géogébra"

2) Conjecturer un minimum pour S(x), et préciser alors la position de P et de Q.
Et pour ca je ne vois pas comment faire !!?

Merci de m'aider...

[_-Gaara-_]

Salut,

Heu tu peux poster ta figure ? stp juste pour voir comment est géogébra :D et comment est la figure car là je ne vois pas trop xD

[Tagogo]

[_-Gaara-_]

lol trop stylé !!! je vais le ddl de suite ;D

Bon pour la formule de l'aire d'un triangle c'est :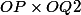 si je ne me trompe pas.

sachant que OQ dépend de OP, on peut écrire que la dimension de OP = x

donc et sachant que les points doivent être alignés, on a Q (AP).

Mais en ce qui concerne la conjecture je pense que tu l'as déjà faite sur ta figure xD P(2;0) et Q(0;4}

ata j'ai une autre idée ^^

[lapras]

Salut,
la conjecture est facile a démontrer tu as l'air en fonction de x (cherche les coordonées de Q avant), puis tu étudie la fonction et c'est bon :happy2:

[Tagogo]

Pour la conjecture je ne sais pas, x peut être égal à la valeur venant juste après 1, (comme x>1), pour obtenir un triangle le plus plat possible...

[Tagogo]

Ça c'est dans la deuxième question:
2) a. exprimer OQ en fonction de x et montrer alors que S(x)= x²/x-1.
b. soit m le minimum conjecturé. montrer qu'effectivement S(x)>m pour x>1

De plus, OQ est dépendent de P, alors comment puis-je trouver Q sans avoir x ?

[_-Gaara-_]

Mais la droite AP est d'équation ax + by + c = 0 ^^ et le vecteur directeur associé à cette droite est v(-b;a)

on sait que A(1;2) et P(x;0) donc -b = x-1 et a = 0-2

donc b = -x+1 et a = -2.

( 2 < c )

euh ata

lapras tu peux aider car là je suis LOST :D

[lapras]

ne nous compliquons pas la vie ;)
Soit Q(xQ , yQ)
la droite (PQ) a pour équation réduite :
y = ax + b
avec b = yQ
cette droite passe par
A(1,2) et P(xP,0)
donc
2 = a*1 + b
0 = xP*a+b
donc a = -b/xP
donc b(1-1/xP) = 2
d'où b = yQ = (2xP)/(xp-1)
donc OQ = (2xP)/(xp-1)
OP = xP
donc
OP*OQ = (2xP²)/(xP-1)
donc l'aire c'est S(x) = xP²/(xP-1)
CQFD
maintenant le minimum conjecturé est 4 cm²
donc
on va montrer que xP²/(Xp-1) - 4 > 0
pour x > 1
c'est maintenant facile a montrer :happy2:

[_-Gaara-_]

Bah ouiiiiiiiiiii voilà !! c'est ce que je voulais faire mais pourquoi n'y a t il pas de c dans l'équation ? oO on a droit de mettre directement la réduite ?? :zen:

ah ok c'est cool héhé

gg lapras :)

[Tagogo]

merci mais je ne comprend pas à partir de cette ligne:
donc b(1-1/xP) = 2

[_-Gaara-_]

2 = a*1 + b = a +b
0 = xP*a+b =
donc a = -b/xP


tu reprends

2 = a*1 + b = a +b et tu remplaces a par -b/xP d

donc 2 = -b/xP + b = b(1-1/xP)

CQFDD

[Tagogo]

oui merci, quand tu a poster la réponse, je venais de compendre. mais on a le droit de mettre un numérateur égal a 0 ? (1-1) ?
et est ce que tu peut me détailler comment on passe de b(1-1/xP) = 2
à b = yQ = (2xP)/(xp-1). ça par contre je n'est pas trouver !