ThSQ a écrit:La notion d'idéal maximal n'est pas officiellement au programme je crois.
Non non, d'ailleurs elle était donnée avec l'exo (c'était mon prof qui me faisait passer l'oral)

Ou bien on est censé le savoir pour les ENS ?
Je ne pense pas que ce soit vraiment très utile, ce genre de choses est forcément redéfini vu le parent pauvre qu'est devenu l'algèbre générale en spé.
Borel-Lebesgue est autrement plus hors programme (il s'agit d'un théorème et non d'une définition !), ... mais pour les ENS, "où personne ne lit jamais le programme", il vaut quand même mieux connaître ça (et plein d'autres résultats d'ailleurs, Dunford-Jordan et autre choses...).
Tu nous donnes les autres exos ?
Tout tournait en fait autour de la notion d'idéal maximal. On demandait d'établir l'équivalence des deux propriétés :
(i)I est maximal,
et (ii)

puis on s'intéressait aux idéaux premiers : on demandait de montrer que tout idéal maximal était premier...
puis on s'intéressait à l'anneau
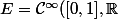)
et à deux de ses idéaux :
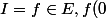=0)
et
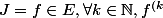}(0)=0)
: on demandait si ces deux idéaux (après avoir vérifié que le deuxième était bien un idéal quand même) étaient premiers, maximaux, ou engendrés par un élément.
