Idéaux maximaux de fonctions
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nonam
- Membre Relatif
- Messages: 163
- Enregistré le: 02 Avr 2008, 17:31
-
 par nonam » 02 Avr 2008, 17:51
par nonam » 02 Avr 2008, 17:51
Bonjour. Je tente depuis quelques temps de montrer ce résultat :
Soit

un corps,

un ensemble non vide,

l'anneau des applications de

dans

Montrer que les idéaux maximaux de

sont les parties de

de la forme :
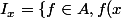 = 0 \})
, avec

J'ai montré que toutes les parties de la forme
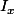
étaient bien des idéaux maximaux. Mais la réciproque me semble nettement plus complexe, et une aide serait vraiment la bienvenue...
Merci d'avance.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 02 Avr 2008, 17:55
par yos » 02 Avr 2008, 17:55
-
nonam
- Membre Relatif
- Messages: 163
- Enregistré le: 02 Avr 2008, 17:31
-
 par nonam » 02 Avr 2008, 18:17
par nonam » 02 Avr 2008, 18:17
Merci pour ces réponses. J'avais fait une recherche et vu cette discussion, mais il ne traite pas le cas de

quelconque.
Et je pense que ce résultat est juste, puisque j'ai trouvé l'exercice dans un livre. Ceci dit, les livres ne disent pas que des choses vrais...
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 02 Avr 2008, 18:35
par ThSQ » 02 Avr 2008, 18:35
nonam a écrit:Merci pour ces réponses. J'avais fait une recherche et vu cette discussion, mais il ne traite pas le cas de

quelconque.
Et je pense que ce résultat est juste, puisque j'ai trouvé l'exercice dans un livre. Ceci dit, les livres ne disent pas que des choses vrais...
Si E n'est pas supposé compact il y a des contrex (cf lien donné par yos)
As-tu des éléments sur la questions que tu posais à la fin du thread yos ? Quid des
idéaux premiers ?
-
nonam
- Membre Relatif
- Messages: 163
- Enregistré le: 02 Avr 2008, 17:31
-
 par nonam » 02 Avr 2008, 19:14
par nonam » 02 Avr 2008, 19:14
Merci ! Et désolée, je n'avais pas regardé avec attention le contre-exple que tu donnais, pensant que tu cherchais à fournir un contre-exemple dans le cas d'applications continues sur un espace topologique. Et je n'avais pas cherché à savoir s'il s'appliquait dans mon cas... encore merci.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 02 Avr 2008, 19:48
par yos » 02 Avr 2008, 19:48
ThSQ a écrit:As-tu des éléments sur la questions que tu posais à la fin du thread yos ? Quid des idéaux premiers ?
Précisément, j'en ai eu il y a quelques heures (après avoir refiler le bébé) :
- premier fermé entraînerait maximal.
- on peut construire P premier non maximal. Pas très simple.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 02 Avr 2008, 20:15
par ThSQ » 02 Avr 2008, 20:15
yos a écrit:Précisément, j'en ai eu il y a quelques heures (après avoir refiler le bébé) :
- premier fermé entraînerait maximal.
- on peut construire P premier non maximal. Pas très simple.
Merci !! Une référence (trouvable en BU

) à proposer ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 02 Avr 2008, 22:12
par yos » 02 Avr 2008, 22:12
Non. J'ai seulement posé la question à des collègues qui ont eu des idées. Je te dirai ça plus tard si j'ai le temps de regarder en détail.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
quelconque.