Correspondance en idéaux. Besoin de quelques explications!
23 messages
- Page 2 sur 2 - 1, 2
Bonjour,
Oui, au temps pour moi, Leon1789 a parfaitement raison.
On reprend donc avec les notations précédentes :
La fonction f: idéaux de définie par
définie par =j^{-1}(J)) associe à un idéal premier de S-1A, un idéal premier de A disjoint de S.
associe à un idéal premier de S-1A, un idéal premier de A disjoint de S.
Il reste à montrer que c'est une bijection.
Injection :=f(J_2)) . Soit x=a/s un élément de J1. a=s.(a/s)=(a/1) =j(a) appartient aussi à J1 (car J1 est un idéal) et a sera donc un élément de
. Soit x=a/s un élément de J1. a=s.(a/s)=(a/1) =j(a) appartient aussi à J1 (car J1 est un idéal) et a sera donc un élément de ) , donc aussi de
, donc aussi de ) par hypothèse. Donc
par hypothèse. Donc 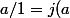 \in J_2) ainsi que (1/s).(a/1)=x.
ainsi que (1/s).(a/1)=x.
On a ainsi montré que=f(J_2)\Rightarrow J_1\subset J_2) . L'inclusion réciproque se démontre de la même façon et l'on a bien f injective (sans utiliser le fait que les idéaux sont premiers)
. L'inclusion réciproque se démontre de la même façon et l'on a bien f injective (sans utiliser le fait que les idéaux sont premiers)
surjection Soit I un idéal premier de A disjoint de S, J l'idéal engendré par j(I) et I'=f(J). Il faut montrer que I=I'
à suivre
Oui, au temps pour moi, Leon1789 a parfaitement raison.
On reprend donc avec les notations précédentes :
La fonction f: idéaux de
Il reste à montrer que c'est une bijection.
Injection :
On a ainsi montré que
surjection Soit I un idéal premier de A disjoint de S, J l'idéal engendré par j(I) et I'=f(J). Il faut montrer que I=I'
à suivre
23 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
