Espaces metriques !

par **barbu23** » 15 Déc 2007, 20:52

parecque les compacts d'un espace vectoriel sont les bornés fermés, et donc la boule fermé est inclus dans elle meme donc, ele est bornée !! c'est ça ?

par **ThSQ** » 15 Déc 2007, 20:56

Tu fais les questions et les réponses ;)

Toutes les boules fermées (de rayon > 0) sont homéomorphes dans tous les evn (voire les evt ?), non ? Si l'une est compacte elles le sont toutes.

par **legeniedesalpages** » 15 Déc 2007, 20:58

oui, c'est ça, et parce qu'on est en dimension finie aussi, me semble -t - il. :)

par **barbu23** » 15 Déc 2007, 21:04

oui, en dimension finie !
Merci à vous 2 !

par **Joker62** » 15 Déc 2007, 21:42

A tout ses posts il fait les questions et les réponses ce barbu :)

par **barbu23** » 16 Déc 2007, 11:29

Bonjour :
La boule unité d'un espace de dimesnion finie est compact ( il y'a m^me équivalence ) .. est ce que cette boule unité est peu importe qu'elle soit ouverte ou fermée ?
Merci d'avance !

par **legeniedesalpages** » 16 Déc 2007, 11:37

en général, non c'est la boule fermée, les compacts son toujours fermés non?
ça peut arriver peut etre que la boule ouverte soit compacte si elle est fermée.

par **barbu23** » 16 Déc 2007, 11:39

oui, tu as raison :++: ! merci beacoup !

par **ThSQ** » 16 Déc 2007, 11:40

Ca arrive qu'une boule ouverte soit fermée (dans des métriques sur des espaces discret par ex.) mais dans des evn c'est pas possible. Une boule ouverte d'un evn n'est jamais fermée.

par **legeniedesalpages** » 16 Déc 2007, 11:43

ou c'est vrai que c'est connexe un evn de dim finie et qu'ici on est en dim finie. C'est le cas aussi pour les evn de dimension infinie? :hein:

par **ThSQ** » 16 Déc 2007, 11:51

Oui je crois bien. Sauf dans un espace de dimension zéro en fait ...

dans B(x,r), boule ouverte, avec y un vecteur non nul (d'où dim > 0), la suite x + y/||y|| * r*(1-1/n) et dans la boule ouverte mais a une limite qui n'est pas dans la boule ouverte.

par **legeniedesalpages** » 16 Déc 2007, 12:00

ah ok, merci ThSQ.

par **ThSQ** » 16 Déc 2007, 12:46

legeniedesalpages a écrit:ah ok, merci ThSQ.

De rien !

C'est la connexité qui joue : un evn est toujours connexe (car convexe) et une boule fermée est toujours fermée donc elle peut pas être fermée ET ouverte.

par **barbu23** » 16 Déc 2007, 16:29

Bonjour :
Soient

et

deux espaces metriques.
Soit

une partie dense de

et

complet.
Soit

uniformement continue.
Alors : il existe un et un seulement prolongement

de

uniformement continue !
Question :
Est ce que vous pouvez me donner la demosntration de cette proposition du cours ! j'ai l'ai pas recopié en classe !
Merci infiniment !!

par **ThSQ** » 16 Déc 2007, 18:21

C'est fait là : http://www.les-mathematiques.net/a/a/b/node26.php3

par **barbu23** » 16 Déc 2007, 19:03

oui, mais elle est pas bien expliqué cette demonstration ! :lol2:

par **Joker62** » 16 Déc 2007, 22:22

C'est le théorème de Complété d'un espace métrique
C'est assez hard à mettre en place de toute manière
Donc bon, autant se contenter de celle proposée

par **legeniedesalpages** » 16 Déc 2007, 22:59

sinon tu peux regarder celle du G.Choquet "Cours de topologgie", ed.Dunod, Ch III, paragraphe 20 (à la fin). Mais elle utilise les modules de continuités, qui ne sont pas toujours introduits dans les cours de topologie.

par **barbu23** » 17 Déc 2007, 13:32

Bonjour :
Voiçi la preuve de notre prof :

,

.

,

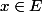uniformement continue.

.

)

Donc, on pose :

.
Il faut verifier que

est continue et que ce prolongement est unique.
Soit :

,

, on a :

:

est uniformement continue.
Si

.

,

(

prolongement definie )
Questions :
Le prof ecrit par hypothèse,

est uniformement continue !! ensuite, dans la demonstration, il dit qu'il faut montrer que

est uniformement continue :lol2: !! je comprends pas !
Merci d'avance , pour vos eclaircissements !!

par **barbu23** » 17 Déc 2007, 16:04

Dans la demonstration, il y'a ça :
" ... il faut montrer que

est continue et que ce prolongement est unique "

est par hypothèse uniformement continue, donc celà implique directement qu'elle est continue !
Après , il écrit preque à la fin de la demonstration que:
"

est uniformement continue "!
elle est dejà uniforemment contniue par hypothèse ! ou est le problème !!
Je voudrai savoir aussi, ça veut dire quoi montrer que le prolongement est unique !
Merci d'avance de votre aide !

Espaces metriques !

Qui est en ligne