Bonjour!
J'ai vu les équations différentielles en cours au début de l'année. Mais je ne me rappelle absolument plus des "histoires" de raccordements.
Le prof nous avait brifés oralement plutôt rapidement, mais j'ai malheureusement plus aucun souvenir.
Pouvez vous m'en faire un petit résumé concis?
Merci!
Equations différentielles: raccordements
10 messages
- Page 1 sur 1
par bitonio » 06 Déc 2007, 20:51
Il y a plusieurs types de raccordements possibles:
- en un point. Tu prolonges par continuité ta fonction (faut voir la classe du raccordement après). Utile en pratique pour chercher une solution maximale de souvenir...
- sur un intervalle où la fonction n'est pas définie... tu peux inventer n'importe quoi ici.
Par exemple, tu peux raccorder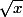
par 0 sur les rééls négatifs... (me demande pas l'utilité!)
- en un point. Tu prolonges par continuité ta fonction (faut voir la classe du raccordement après). Utile en pratique pour chercher une solution maximale de souvenir...
- sur un intervalle où la fonction n'est pas définie... tu peux inventer n'importe quoi ici.
Par exemple, tu peux raccorder
par busard_des_roseaux » 06 Déc 2007, 21:19
bonsoir,
regardons d'abord le prolongement par continuité en
on pose:
 = \lim_{x \rightarrow 0^+} \, f(x)=\lim_{x \rightarrow 0^-} \, f(x))
et
=f(x))
ailleurs.
(si les deux limites sont égales).
Dans ce cas , le prolongement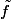
est continue
en zéro.
Ensuite si le quotient:
}{x})
a une limite quand 
, le prolongement est dérivable.
D'après le thm des accroissements finis, une condition suffisante pour qu'il en soit ainsi est l'existence et l'égalité des deux limites:
=\lim_{x \rightarrow 0^-} f '(x))
Une condition nécéssaire et suffisante pour que f admette un prolongement
en est le critère de Cauchy local:
-f(x')|< \epsilon)
En effet, la condition est nécéssaire car le prolongement doit être uniformément continu sur un voisinage compact de zéro.
La condition est suffisante , car si deux suites)
et )
tendent vers zéro, leurs images sont des suites convergentes,
de même limite car on peut mixer les deux suites. (argument subtil)
et donc toutes les suites de points tendant vers zéro donneront le même prolongement.
cordialement,
regardons d'abord le prolongement par continuité en
on pose:
et
(si les deux limites sont égales).
Dans ce cas , le prolongement
en zéro.
Ensuite si le quotient:
D'après le thm des accroissements finis, une condition suffisante pour qu'il en soit ainsi est l'existence et l'égalité des deux limites:
Une condition nécéssaire et suffisante pour que f admette un prolongement
en
En effet, la condition est nécéssaire car le prolongement doit être uniformément continu sur un voisinage compact de zéro.
La condition est suffisante , car si deux suites
de même limite car on peut mixer les deux suites. (argument subtil)
et donc toutes les suites de points tendant vers zéro donneront le même prolongement.
cordialement,
par Clark_ » 06 Déc 2007, 22:31
hum, merci à vous deux pour vos réponses disons... formelles!
C'est très complet, néanmoins certains passages m'échappent. Pourriez vous me faire la démonstration sur un exemple simple? Je pense que ça me parlera bien plus.
Merci!
C'est très complet, néanmoins certains passages m'échappent. Pourriez vous me faire la démonstration sur un exemple simple? Je pense que ça me parlera bien plus.
Merci!
par bitonio » 06 Déc 2007, 22:38
Un exemple:
}{x})
se prolonge par continuité en 0 par 1 et on obtient une nouvelle fonction définie sur R
par busard_des_roseaux » 06 Déc 2007, 22:39
par busard_des_roseaux » 06 Déc 2007, 23:03
L'exemple de Bitonio est 
ie, son prolongement par continuité admt des dérivées de tous ordres qui se "recollent" (on voit ça car en plus sa fonction est développable en série entière) et mon exemple est juste
, cad que le prolongement n'est pas dérivable , la courbe admet un point anguleux.
ie, son prolongement par continuité admt des dérivées de tous ordres qui se "recollent" (on voit ça car en plus sa fonction est développable en série entière) et mon exemple est juste
par bitonio » 06 Déc 2007, 23:08
busard_des_roseaux a écrit:L'exemple de Bitonio est
On voit tout de suite les BG :we: (humour)
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :