Isométrie
18 messages
- Page 1 sur 1
Isométrie
Bonjour voilà j'ai un exercice à faire qui est le suivant :
(Théorème de Poincaré)
1) Soit (E,d) compact et f:(E,d)->(F,d') une bijection continue.
Monter que f est un homéomorphisme.
2) Soit g:(E,d)->(E,d) une isométrie.
( g isométrie <=> Pour tout x,x' de E on a d(g(x),g(x'))=d(x,x') )
Monter que g est surjective.
Pour le 1) on montre que f est fermée en utilisant les propriètés des fermés dans les compacts et la continuité.
(Un homéomorphisme est une application continue, bijective et fermée)
Pour le 2) j'ai montrer que c''est injectif et continue(1-lipschtzienne) mais je ne vois pas comment montrer la surjectivité.
Si quelqu'un pouvait me donner des renseignement se serait sympa.
Merci
(Théorème de Poincaré)
1) Soit (E,d) compact et f:(E,d)->(F,d') une bijection continue.
Monter que f est un homéomorphisme.
2) Soit g:(E,d)->(E,d) une isométrie.
( g isométrie <=> Pour tout x,x' de E on a d(g(x),g(x'))=d(x,x') )
Monter que g est surjective.
Pour le 1) on montre que f est fermée en utilisant les propriètés des fermés dans les compacts et la continuité.
(Un homéomorphisme est une application continue, bijective et fermée)
Pour le 2) j'ai montrer que c''est injectif et continue(1-lipschtzienne) mais je ne vois pas comment montrer la surjectivité.
Si quelqu'un pouvait me donner des renseignement se serait sympa.
Merci
On avait même traité une version plus hard t'en souviens-tu?
http://www.maths-forum.com/showthread.php?t=24301&highlight=surjective
http://www.maths-forum.com/showthread.php?t=24301&highlight=surjective
yos a écrit:Prends x dans E, la suite fofofo...of (x), extrait une sous-suite convergente, et écris qu'elle est de Cauchy.
Merci c'est comme ça que j'ai fait. cela nous donne que x appartient à la fermeture de Im g, qui est fermé donc x appartient à im g
d'où la surjectivité. :we:
Merci.
Sinon vous connaissez le th de poincaré en rapport avec cet exo?
J'ai cherché mais je trouve que des trucs de physique il a fait pas mal de chose.
Oui il y a les meme hypothèses :happy2:
J'ai encore une petite question, merci pour votre patience, qu'elle condition dois-je poser sur la sous-suite pour que sa marche ?
Soit Y appartennant à E
xn=g°g°...(y) n fois
g continue (1-lipschitzienne) et E compact donc Im g compact
donc xn a une sous suite qui converge ( xp(n) )
Quel précaution doit t'on prendre sur p(n) pour que sa marche ?
Je suis passé ce matin au tableau et le prof ma dit que je devais mettre une hypothèse supplémentaire :livre:
Mais il m'a dit que j'étais sur la bonne voie :we:
J'ai encore une petite question, merci pour votre patience, qu'elle condition dois-je poser sur la sous-suite pour que sa marche ?
Soit Y appartennant à E
xn=g°g°...(y) n fois
g continue (1-lipschitzienne) et E compact donc Im g compact
donc xn a une sous suite qui converge ( xp(n) )
Quel précaution doit t'on prendre sur p(n) pour que sa marche ?
Je suis passé ce matin au tableau et le prof ma dit que je devais mettre une hypothèse supplémentaire :livre:
Mais il m'a dit que j'étais sur la bonne voie :we:
yos a écrit:Cauchy : Pour m>n>N,mais
(puisque
est une isométrie).
Oui j'ai fait
Ensuite j'affirme que x est limite d'une sous suite(valeur d'adhérence), donc il appartient à la fermeture de Im g qui est fermé donc il appartient à im g
Mais on m'a demandé de préciser sur p(n).
Si tu vois ce qu'il voulait dire ?
Désolé j'ai du mal avec les balises
Merci :we:
En fait il suffisait juste de poser
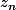 =
=-p(n)})
donc est adhérent à Im g qui est fermé ce qi prouve la surjectivité. Je sais pas pourquoi je me suis pris la tete avec cette histoire de sous suite
Et puis le fait d'etre au tableau m'a empeché de réflechir correctement :lol2:
En tout cas je vous dis merci à tous deux :++:
donc est adhérent à Im g qui est fermé ce qi prouve la surjectivité. Je sais pas pourquoi je me suis pris la tete avec cette histoire de sous suite
Et puis le fait d'etre au tableau m'a empeché de réflechir correctement :lol2:
En tout cas je vous dis merci à tous deux :++:
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
