Calcul modulaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 01 Déc 2007, 21:17
par juve1897 » 01 Déc 2007, 21:17
Bonsoir,
je voulais savoir si qqun pouvait m'expliquer comment est ce qu'on résout une équation du type:

Merci beaucoup.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 01 Déc 2007, 21:23
par ThSQ » 01 Déc 2007, 21:23

est jamais divisible par 3.
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 01 Déc 2007, 21:28
par juve1897 » 01 Déc 2007, 21:28
ThSQ a écrit:
est jamais divisible par 3.
Merci pour ta réponse, mais je ne comprends pas en quoi cela pourrait m'aider à résoudre mon équation.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 01 Déc 2007, 21:30
par ThSQ » 01 Déc 2007, 21:30
juve1897 a écrit:Merci pour ta réponse, mais je ne comprends pas en quoi cela pourrait m'aider à résoudre mon équation.
Si c'est pas divisible par 3 comment ça pourrait bien l'être par 135 ...
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 01 Déc 2007, 21:34
par juve1897 » 01 Déc 2007, 21:34
ThSQ a écrit:Si c'est pas divisible par 3 comment ça pourrait bien l'être par 135 ...
Merci,
mais là vous me donnez la réponse, sans explication, alors que le but de mon topic était plutôt d'obtenir une méthode de résolution, que je pourrais appliquer sur d'autre exemple.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 01 Déc 2007, 22:56
par ThSQ » 01 Déc 2007, 22:56
Je sais pas s'il y a une méthode à part regarder modulo les diviseurs de 135.
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 02 Déc 2007, 15:00
par juve1897 » 02 Déc 2007, 15:00
ThSQ a écrit:Je sais pas s'il y a une méthode à part regarder modulo les diviseurs de 135.
Mais comment avez vous fait pour trouver qu'il n' y a pas de solutions ?
Comment feriez vous avec

Pourriez vous dans ce cas là me détailler votre démarche de calcul.
Merci de votre aide.
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 02 Déc 2007, 19:15
par juve1897 » 02 Déc 2007, 19:15
j'ai un examen important dans qq jours et j' apprécierai que qqun m'aide un peu.
Alors, j'ai fait des recherches sur mon problème et j'ai pu voir qu'une manière de résolution existe mais en passant par "les formules de cardan".
Or je n'ai jamais étudié ces formules, et le principe m'a l'air bien compliqué.
Est ce qu'il y aurait qqun pour me donner une methode de résolution sans utiliser ces formules ?
Merci d'avance.
 par busard_des_roseaux » 02 Déc 2007, 19:56
par busard_des_roseaux » 02 Déc 2007, 19:56
bonsoir,

Si p est premier, Z/pZ est un corps
on peut supposer le polynome unitaire et faire une division des polynomes dans Z/pZ[X]. A mon avis, il y a au plus trois racines dans ce cas-là.
Si p est composé, l'équation peut avoir strictement plus de 3 solutions.
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 02 Déc 2007, 20:07
par juve1897 » 02 Déc 2007, 20:07
busard_des_roseaux a écrit:bonsoir,

Si p est premier, Z/pZ est un corps
on peut supposer le polynome unitaire et faire une division des polynomes dans Z/pZ[X]. A mon avis, il y a au plus trois racines dans ce cas-là.
Merci pour ta réponse, je commençais à désespérer.
Cependant, je n'ai pas trop compris ton raisonnement.
J'ai reflechit de mon coté et j'ai eu l'idée d'utiliser la propriété suivante
Si

et

Alors

Or moi j'ai

donc j'ai pensé que cela pouvait donner:




Donc je peux conclure que cette équation n'a pas de solution car l'équivalence

est fausse.
Est ce que mon raisonnement est bon ???
Merci.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 02 Déc 2007, 22:21
par ThSQ » 02 Déc 2007, 22:21
J'ai vu des résultats zoulis sur les congurences mod
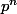
des polynomes (lemmes de Hensel,
http://en.wikipedia.org/wiki/Hensel%27s_lemma) mais j'ignore s'il y a des résultats dans le cas général.
Enfin c'est pas bien compliqué.
Pour regarder si un polynome P peut être divisible par n il suffit de regarder les restes de P(0), P(1), ..., P(n-1). Si ils sont tous différents de zéros c'est jamais divisible par n.
Ici regarde que ton polynome est jamais divisible par 5 : calcule P(i) mod (5) pour i=0..4.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 02 Déc 2007, 23:08
par yos » 02 Déc 2007, 23:08
Pour résoudre f(x)=0 dans Z/nZ, tu remplaces x par chacun des n éléments de Z/nZ : si ça fait 0, ... je dois continuer?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités