Calcul modulaire.

[juve1897]

bonsoir,

je dois trouver les deux derniers chiffre en base 10 de :

• 
• 

En fait j'ai pensé qu'il fallait faire:

or 100 n'est pas premier
donc

Est ce une bonne solution

[Euler911]

Bonsoir,

Qu'entends-tu par dernier chiffre??? Celui de dizaines et celui des unités

[juve1897]

Bonsoir,

Qu'entends-tu par dernier chiffre??? Celui de dizaines et celui des unités

en fait je pense que l'exo demande de trouver les deux derniers chiffre du nombre cad celui des dizaines et unités

Ex: 1238
et ben il faut répondre 38

[Euler911]

Pour les unités tu peux remarquer qu'il y a un cycle: {3,9,7,1,} ...

[miikou]

pour le chiffre des unites c'est simple tu congrues modulo 10.
pour le chiffre des dizaines congrues modulo 100 ;)

[juve1897]

pour le chiffre des unites c'est simple tu congrues modulo 10.
pour le chiffre des dizaines congrues modulo 100

mince je pensais que faire congru 100 me donnerait en mm temps le chiffre des dizaines et celui des unités

[juve1897]

Pour les unités tu peux remarquer qu'il y a un cycle: {3,9,7,1,} ...

tout à fait, j'ai calculé tout à l'heure modulo 10 j'ai trouvé 1

[skilveg]

Tu peux aussi remarquer que , donc, comme 3 est premier à 100, le théorème de Lagrange nous donne directement ... Se rabattre coûte que coûte sur le théorème chinois n'est pas toujours une bonne idée :langue:

[Euler911]

EDIT:***J'aurais mieux fait de me taire***

[juve1897]

Tu peux aussi remarquer que , donc, comme 3 est premier à 100, le théorème de Lagrange nous donne directement ...

Excuse moi, mais tu es allé trop vite pour moi.
Comment as tu trouvé l'indicatrice en 2 temps trois mouvements ?
Et puis je ne connais pas le theo de lagrange.

Peux tu detailler si cela ne te derange pas ?

[Euler911]

mince je pensais que faire congru 100 me donnerait en mm temps le chiffre des dizaines et celui des unités

Travailler modulo 100 à pour but de donner les 2 derniers chiffres d'un nombre... n'oublions
que dans b est le reste de la division de a par 100

[skilveg]

Non bah si tu ne connais pas encore le théorème de Lagrange ce n'est pas grave... J'explique quand même ce que je fais:

On sait que pour tout entier l'indicatrice d'Euler de est le produit (où la notation signifie que le produit est fait sur tous les facteurs premiers). D'où sa valeur en 100 dont les seuls facteurs premiers sont 2 et 5.

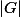
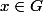
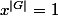
Théorème de Lagrange: soient un groupe fini et un sous groupe de ; alors divise . En particulier, si , alors (considérer le sous groupe ).

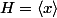
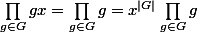
(Démonstration du cas particulier, et dans le cas particulier où est abélien: l'application de dans qui à associe est une permutation. Donc et en simplifiant .)

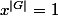
Application dans le cas qui nous intéresse: le groupe considéré est qui est d'ordre et qui contient bien 3 puisque 3 et 100 sont premiers entre eux. Donc .

[juve1897]

Travailler modulo 100 à pour but de donner les 2 derniers chiffres d'un nombre... n'oublions
que dans b est le reste de la division de a par 100

donc j'avais bien raison ???

[Euler911]

donc j'avais bien raison ???

Oui .

[Euler911]

Non bah si tu ne connais pas encore le théorème de Lagrange ce n'est pas grave... J'explique quand même ce que je fais:

On sait que pour tout entier l'indicatrice d'Euler de est le produit (où la notation signifie que le produit est fait sur tous les facteurs premiers). D'où sa valeur en 100 dont les seuls facteurs premiers sont 2 et 5.
[...]

Application dans le cas qui nous intéresse: le groupe considéré est qui est d'ordre et qui contient bien 3 puisque 3 et 100 sont premiers entre eux. Donc .

:doh: :doh: :ptdr:

[juve1897]

Non bah si tu ne connais pas encore le théorème de Lagrange ce n'est pas grave... J'explique quand même ce que je fais:

On sait que pour tout entier l'indicatrice d'Euler de est le produit (où la notation signifie que le produit est fait sur tous les facteurs premiers). D'où sa valeur en 100 dont les seuls facteurs premiers sont 2 et 5.

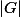
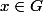
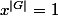
Théorème de Lagrange: soient un groupe fini et un sous groupe de ; alors divise . En particulier, si , alors (considérer le sous groupe ).

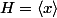
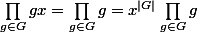
(Démonstration du cas particulier, et dans le cas particulier où est abélien: l'application de dans qui à associe est une permutation. Donc et en simplifiant .)

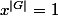
Application dans le cas qui nous intéresse: le groupe considéré est qui est d'ordre et qui contient bien 3 puisque 3 et 100 sont premiers entre eux. Donc .

Merci pour les explications (auxquelles je n'ai pas tout compris), mais pour me rassurer, à quel niveau apprend on ces théorèmes ???

[skilveg]

Euh, bonne question... Le calcul de on doit le voir à peu près en même temps que l'indicatrice d'Euler, et le théorème de Lagrange, quand on commence à faire de la théorie des groupes...

Lagrange est hors programme en taupe je crois, mais tout le monde le fait. En fac il doit se voir en licence mais je ne sais pas trop en quelle année.

Si je peux éclaircir ce que je raconte là-dessus, n'hésite pas à demander...

[juve1897]

Euh, bonne question... Le calcul de on doit le voir à peu près en même temps que l'indicatrice d'Euler, et le théorème de Lagrange, quand on commence à faire de la théorie des groupes...

Lagrange est hors programme en taupe je crois, mais tout le monde le fait. En fac il doit se voir en licence mais je ne sais pas trop en quelle année.

Si je peux éclaircir ce que je raconte là-dessus, n'hésite pas à demander...

Oui s'il te palit.
en plus j'ai l'affichage (des balises latex) qui deconne je vois pas les formules correctement.

En fait moi je suis en Licence d'info (3eme année) et on a appris l'indicatrice pour les nombres premiers, et les petit nombre (à faire à la main 1,2,3 ...)

Donc si tu pouvais m'expliquer une fois de plus j'apprecirai.

Merci.
Je trouve ça sympa que des personnes comme toi, prennent leur temps pour expliquer aux autres (mm 10 fois s'il le faut).

[skilveg]

Alors: comment calculer ?

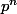
1) Déjà, tu as vu que pour premier. On peut généraliser: si en plus est un entier, . Pourquoi? est le nombre d'entiers entre 1 et premiers à ; dans , les seuls entiers qui ne sont pas premiers à sont les multiples de , et il y en a .

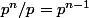
2) Si et sont premiers entre eux, alors (on dit que l'indicatrice d'Euler est multiplicative). En effet, est le cardinal de . Par le théorème chinois, ce groupe est isomorphe à , qui est de cardinal .

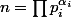
3) Avec ces deux ingrédients, on peut calculer en fonction de la décomposition en facteurs premiers de : si , alors par multiplicativité , donc finalement .

C'est plus clair?

[juve1897]

Je tiens d'abord à vous remercier énormément pour vos explications ainsi que pour le temps que vous m'accordez.

En fait j'ai un gros soucis avec l'affichage, le code LATEX ne s'affiche pas du tout, et j'ai le forum entier qui s'affiche de manière assez bizarre.

Donc je pense que je vais relire un peu plus tard vos explication.

Sinon puis je vous demander de l'aide concernant mon topic "Petite récurrence"
La personne qui m'aidait est allée se coucher, et je n'ai pas vraiment compris ces explications.

Je vous remercie encore.