colmment demontrons que
T^2N-1 est superieur a N(T²-1)
et les variation d'une fonction qui a pour derivee
-1+X²-X^3+X^4-X^5+X^+5...+X^N-1
Inegalite a etablir
5 messages
- Page 1 sur 1
colmment demontrons que
T^2N-1 est superieur a N(T²-1)
Je traduis, en respectant les règles de priorité des opérations, en :
) ?
?
J'imagine qu'on suppose t>0
C'est très simple. Il suffit d'étudier les variations de la fonction différence.
Soit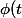=t^{2n}-1-n(t^2-1))
 est dérivable sur
est dérivable sur  et :
et :
=2nt(t^{2n-2}-1)) dont le signe est évident.
dont le signe est évident.
Donc est décroissante sur [0;1] puis croissante.
est décroissante sur [0;1] puis croissante.
Or=0)
Donc est toujours positive
est toujours positive
Et l'inégalité est vraie.
Sauf erreur.
Nicolas
T^2N-1 est superieur a N(T²-1)
Je traduis, en respectant les règles de priorité des opérations, en :
J'imagine qu'on suppose t>0
C'est très simple. Il suffit d'étudier les variations de la fonction différence.
Soit
Donc
Or
Donc
Et l'inégalité est vraie.
Sauf erreur.
Nicolas
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
