Continuité.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Purrace
- Membre Rationnel
- Messages: 536
- Enregistré le: 10 Déc 2006, 16:06
-
 par Purrace » 01 Sep 2007, 13:31
par Purrace » 01 Sep 2007, 13:31
Bonjour ,
Je bug sur un nouvel exercice , là , je pense trés difficile :
Voila l'énoncé :


--
)
si
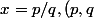)
appartenant à

-- 0 si

appartient à

.
Voila si vous avez des pistes de commencement à me suggeré?
Merci d'avance.
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 01 Sep 2007, 13:39
par Sylar » 01 Sep 2007, 13:39
Y a pas de question ?!
-
Purrace
- Membre Rationnel
- Messages: 536
- Enregistré le: 10 Déc 2006, 16:06
-
 par Purrace » 01 Sep 2007, 13:54
par Purrace » 01 Sep 2007, 13:54
Veillez m'excuser , j'ai oublier la question mais comme vous l'avez deduit , il faut etudier la continuité de l'application en tout point.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 01 Sep 2007, 13:58
par fahr451 » 01 Sep 2007, 13:58
bonjour
quelle est l'image de 0 ?
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 01 Sep 2007, 14:43
par lapras » 01 Sep 2007, 14:43
Salut,
dans la partie lycée récemment on a eu un post avec une fonction similaire qui prenait une valeur défibie selon la nature de la variable (irrationnel ou rationnel).
-
Purrace
- Membre Rationnel
- Messages: 536
- Enregistré le: 10 Déc 2006, 16:06
-
 par Purrace » 01 Sep 2007, 15:41
par Purrace » 01 Sep 2007, 15:41
L'enoncé ne donne pas l'image pour x=0 , mais je tient à rappeller que c'est un exercice de SUP et non du secondaire.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 01 Sep 2007, 16:05
par aviateurpilot » 01 Sep 2007, 16:05
Purrace a écrit:Bonjour ,
Je bug sur un nouvel exercice , là , je pense trés difficile :
Voila l'énoncé :


--
)
si
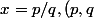)
appartenant à

-- 0 si

appartient à

.
Voila si vous avez des pistes de commencement à me suggeré?
Merci d'avance.
soit
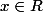
si

soit
)
une suite qui converge ves x
il est clair de voir que les terme irrationnel de
)
ne pose pas de probleme puisque leurs image
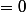
alors on peux suppose que toutes la suite est rationnel

et
=1)
.
est on a donc
=\lim_{n\to +\infty}\frac{1}{p_n+q_n}=0=f(x))
car

d'ou f est continue en x forall

mtn en passe à

suppsoons que f continue en x tel que
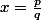
ou
=1)
(et soit
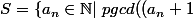q,a_np)=1,a_{n+1}>a_n,a_1=1})
)
donc on a
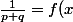=\lim_{n\to\infty}f(\frac{pa_n}{q(a_n+1)})=\lim_{n\to\infty}\frac{1}{a_n(p+q)+q}=0)
(absurde)
d'ou f n'est pas continue en x ,

-
Purrace
- Membre Rationnel
- Messages: 536
- Enregistré le: 10 Déc 2006, 16:06
-
 par Purrace » 01 Sep 2007, 17:15
par Purrace » 01 Sep 2007, 17:15
Bravo aviateurpilot , meme si j'ai du mal a comprendre la demonstration.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 01 Sep 2007, 17:22
par Nightmare » 01 Sep 2007, 17:22
Ca sert à quoi t'introduire ton ensemble S ici?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 01 Sep 2007, 17:32
par fahr451 » 01 Sep 2007, 17:32
en effet
pour x=p/q
il existe une suite xn d'irrationnels qui tend vers x
f(xn) = 0 ne tend pas vers 1/(p+q) =f(x) "ainsi" la discontinuité en x
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 01 Sep 2007, 17:50
par aviateurpilot » 01 Sep 2007, 17:50
Purrace a écrit:Bravo aviateurpilot , meme si j'ai du mal a comprendre la demonstration.
pour

j'ai montrer que pour tt les

suites qui converge vers x
)
aussi copnverge vers
)
d'ou f est continue en

-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 01 Sep 2007, 17:54
par aviateurpilot » 01 Sep 2007, 17:54
Nightmare a écrit:Ca sert à quoi t'introduire ton ensemble S ici?
j'ai just former une suite

tel que
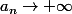
et
,pa_n)=1)
pour avoir le droit d'ecrire
})=\frac{1}{a_n(p+q)+q})
et apres j'ai utilisé la suite
})
et j'ai trouvé que

mais
)
ne tend pas vers x, d'ou f n'ets pas continue en x
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
--
si
appartenant à

appartient à
.