Passer de bonnes vacances

[titi]

BOnjour à tous ça va bien ????

Bon voila j'ai un problème sur cet exercice assez compliqué qui peut m'aider ????


Fonction circulaire

Soit f la fonction définie sur R par f(x)= cos2x - 2racine2 cos x

1°] Montrer que f est périodique de période 2pie

2°] Etudier la parité de f puis justifier que l'étude de f sur l'intervalle [0; pie] permet de représenter graphiquement f .

3°] Vérifier que f '(x)= -4sin x(cos x- racine2 /2) puis déterminer le signe de f '(x) sur [0;pie];
Dresser le tableau de variation de f sur [0; pie]

4°] Dresser la courbe (Cf) sur l'intervalle [ -pie; pie] en expliquant la construction .


Merci d'avance pour votre aide !!! Et bon courage parce que moi ... :marteau: :marteau: :briques:

[Galt]

Quelle question pose problème ?

[titi]

A vrai dire sans paraitre pour un faignant vraiment toute les questions me sont difficiles et je ne trouve aucune méthode même grâce au court sous mes yeux pour résoudre ce problème !!!!


Si quelqu'un pouvait m'aider je lui serait très reconnaissant !!! :zen: :zen: :zen:

[Galt]

?
Montrer que est péridique de période , c'est montrer que . On sait que donc ...
Etudier la parité, c'est voir ce qu'on peut dire de en fonction de
Calculer la dérivée...
Utiliser la formule donnant
Etudier un signe...

[allomomo]

Salut,

Tu as besoin de cette formule à la deuxième question (pour la transformation):

Pour tout x, on

[titi]

Bonjour à tous !!!

Non je n'y arrive pas personne peut à vrai dire plus que m'aider je sais que ce n'est pas très pédagogique mais bon pour une fois ...

J'y ai passé presque toute la journée pourquoi ??? RIEN aucun calcul...


P.S. : je suis à l'agonie personne pour me tendre une GRANDE perche lol


Merci d'avance

[Alpha]

Salut, titi,

peux-tu préciser quelles sont les questions qui te posent problème? Par exemple, ça m'étonnerait que la question 1 te pose problème.

En tout cas, précise où se trouve ta difficulté, et fais nous part, au moins rapidement, de ce que tu as tenté de faire, et de ce que tu ne comprends pas, sinon, je ne vois pas comment nous pourrions t'aider de façon constructive.

Cordialement

[titi]

ce sont les questions 2 et 3 que je n'arrive po du tout à faire

[Alpha]

Salut, titi,

étudier la parité d'une fonction se fait en plusieurs étapes :

déjà, tu vérifies que l'ensemble de définition deest symétrique par rapport à 0, par exemple si l'ensemble de définition de est ]-1, 0] U [3 ; + l'infini[, il est clair que le domaine de définition n'est pas symétrique, donc la fonction ne peut être ni paire ni impaire.

Ensuite, si l'ensemble de définition est bien symétrique,

tu calcules, pour tout x de cet ensemble, .

Si , alors la fonction est paire.
Si , elle est impaire.

Soit la courbe représentative de la fonction, la parité se traduit par le fait que présente une symétrie axiale rapport à l'axe (Oy), l'imparité par le fait que présente une symétrie centrale de centre O.

Etudier la parité de , c'est vérifier si elle est paire ou impaire.

Cordialement

[titi]

et la 3ème question stp merci bien sûr de ta précieuse aide

[Chimerade]

et la 3ème question stp merci bien sûr de ta précieuse aide

Bon ! Troisième question : le calcul de la dérivée. f est la somme de deux fonctions : la dérivée d'une somme est la somme des dérivées. Tu es donc ramené au calcul de la dérivée de cos(2x) et à celui de la dérivée de .

cos(2x) est la fonction composée de deux fonctions : u(x)=2x et v(u)=cos(u). La dérivée de la composée de deux fonctions est le produit des dérivées de chacune d'elles. La dérivée de u(x)=2x est 2. La dérivée de v(u)=cos(u) est -sin(u). La dérivée de cos(2x) est donc -2sin(2x). Et ainsi de suite.

Si tu ne sais pas bien ce qu'est une dérivée, il est normal que tu ne comprennes rien à tout cela. Si par contre tu as déjà eu un cours sur les dérivées, toutes ces règles de calcul font partie du cours...

Bon courage...

[titi]

tu peux me souhaiter du courage j'ai absolument rien compris et je dois l'avoir fini pour 14h parce que mon père rentre du boulot et prend les exos qu'il m'a donné et si je les ai pas fait il engueule ma mè ....alors .......

merci quand même mais bon.... Avec les grèves sur la loi Fillon qui a eu cette année et mon prof qui était souvent malade j'ai passé une année de maths horrible j'ai la moitié du programme en tête et même en m'aidant de bouquins quand on t'à pas expliqué ça ne veut pas rentrer!!! y'a t'il quelqu'un qui

me ferait l'exercice et qui m'en donnerait en contre-partie 2 sur le second degrés par exemple que je ferais pour m'excuser d'avoir eu le cooriger de cet exercice ??????? Je sais que ce que je demande est gonfle mais quand on a des problèmes ((pas seulement en maths))) un peu d'aide de quelque part cela fait un très grand bien : une bouffée d'air !!! :mur: :help: :mur: :help:

[Alpha]

Salut, titi,

sais-tu, oui ou non, ce qu'est une dérivée, et comment on la calcule? Connais-tu les dérivées des fonctions cosinus et sinus?

Il faut que tu précises très clairement quelles sont les choses que tu ne connais pas et quelles sont les choses que tu ne comprends pas.

[titi]

Bonjour Alpha j'ai le cours polycopiés mais à vrai dire je vais faire ça cette après-midi revoir toute les leçons dont celle que je n'ai jamais apprises ... Mais avant 14h il me faut à tout pris le coorigés de cet exercice car je dois le reprendre et voir pourquoi je n'ai pas su le faire...comme je t'ai expiqué la raison précédemment!!!


Avec tout mon respect titi!!!

[Alpha]

Tu n'as pas répondu à mes questions :

Sais-tu ce qu'est une dérivée? Sais-tu calculer une dérivée? Connais-tu les dérivées de cosinus et de sinus?

J'attends.

[titi]

oui alpha je sais tout cela mais je n'arrive pas dans le cas présent à l'utiliser

[titi]

Alpha je t'en supplie j'ai besoin d'aide assez rapidemment je t'en serais très reconnaissant stp stp ou même les 1500 participants aux forums j'ai besoin d'aide d'urgence merci de votre compréhension :cry: :cry: :cry: :cry:

[Alpha]

Peut-être alors que tu ne connais pas la dérivée d'une fonction composée.

Avec cela, ça devrait aller :

Soit une fonction et une fonction telles que l'ensemble d'arrivée de soit inclus dans l'ensemble de départ de ,

alors la dérivée de la fonction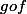 (qui est la fonction qui à associe est égale à ,

donc la fonction dérivée de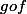 est la fonction qui à x associe .

Par exemple, si je prends f et g définies ainsi :





La fonction composée de par est .

En appliquant ceci à la question où il faut dériver, tu trouves le résultat.

Utilises aussi le fait que la dérivée d'une somme de fonctions est la somme des dérivées de ces fonctions :

Si j'ai une fonction , une fonction et une fonction ,

et que , c'est-à-dire que est la fonction qui à tout de son ensemble de définition,

associe ,

alors .

Tu devrais pouvoir te débrouiller avec ça.

[titi]

merci beaucoup de ta précieude aide bon je dois me mettre au boulot !!!!! :zen: :zen: :zen: :zen:

[Alpha]

Voilà, je t'envoie la solution :

En appliquant ce que j'ai dit plus haut, il vient :

Dérivée :

(on utilise le fait que la dérivée du cosinus est -sinus, et celle de sinus est cosinus)

Et comme sin(2x)=2sin(x)cos(x), on peut écrire :






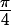La dérivée est un produit de deux facteurs. Pour sin(x) on sait que c'est positif pour x entre 0 et . Pour le deuxième facteur, on pourrait essayer de factoriser davantage, mais cela n'est pas nécessaire. En effet, entre 0 et , la fonction cosinus est décroissante. Elle varie de 1 à -1 et passe donc une seule fois par la valeur qui est le cosinus de . Avec tout ça, tu devrais trouver le signe de f '(x) pour l'intervalle étudié.


Voilà. Avec la très grande participation de Chimerade (que je remercie fortement! :happy3:), qui avait déjà rédigé la solution et qui me l'a fournie pour que j'aille plus vite, étant donnée la contrainte de temps (doit être fait avant 14H).

Cordialement