Ces bonnes vieilles suites

par **Frednight** » 29 Sep 2009, 17:48

Bonjour

Je serais très reconnaissant si vous pouviez m'aider pour cette exercice sur les suites :

On me demande simplement de calculer

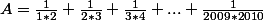
J'ai commencé la résolution comme ceci :

Soit

Alors

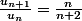
Seulement, je n'arrive pas à prolonger le raisonnement qui me permettrait de trouver la raison de cette suite qui me permettrait ensuite d'en faire l'addition des termes consécutifs.

Quelqu'un pourrait-il m'aider?

par **girdav** » 29 Sep 2009, 17:53

Bonjour.
L'idée consiste à écrire

sous la forme

.

par **Frednight** » 29 Sep 2009, 18:48

par **Frednight** » 29 Sep 2009, 18:58

mas je ne parviens toujours pas à prolonger....

des conseils?

par **Nightmare** » 29 Sep 2009, 19:02

Réfléchis un petit peu, essaye de réécrire la somme qu'on te demande de calculer en utilisant le résultat que tu viens de trouver !

par **bombastus** » 29 Sep 2009, 19:03

Salut,

avec cette nouvelle formule
calcule u1+u2 = ???
puis :
u1+u2+u3 = ???
que remarques-tu?
que vaut u1+u2+...+u(n-1)+un = ???

par **Frednight** » 29 Sep 2009, 19:17

Je dirais, après avoir observé

, que

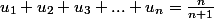
cependant, je ne sais comment m'y prendre :

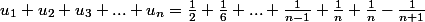
je ne vois pas comment avancer

par **Frednight** » 30 Sep 2009, 16:22

J'aimerais juste un éclaircissement au niveau de la seconde partie de l'égalité, lorsque 'on additionne les valeurs de

,

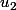
etc

par **girdav** » 30 Sep 2009, 16:25

Il y des termes qui se détruisent. Comme par calculer

puis

et enfin

pour voir le truc.

par **Frednight** » 30 Sep 2009, 17:46

merci à tous pour votre aide

Ces bonnes vieilles suites

Ces bonnes vieilles suites

Qui est en ligne