Suite d'ensembles !

par **BQss** » 13 Aoû 2007, 01:14

barbu23 a écrit:D'accord, bonne nuit !!

Bonne nuit! demain t'auras l'esprit plus clair je pense :happy2: .

par **barbu23** » 13 Aoû 2007, 01:15

mais si on veut maintenant passer à l'inclusion comment faire ?!!

par **barbu23** » 13 Aoû 2007, 01:17

D'accord !

par **BQss** » 13 Aoû 2007, 01:18

BQss a écrit:pour montrer que lim An= A --> limsup=liminf

tu as deja:
s'il existe n0 tel que n>n0 x appartient à An alors:
x appartient à l'union des An pour n>=m quelque soit m>n0 (i.e appartient a tous) et donc à l'intersection des An pour n>m0 qui est inclus dans l'union sur m des intersections sur m>n0.
Donc x appartient alors aussi à liminf An et lim An=A est inclu dans liminf An.
Or on sait que liminf An est inclu dans limAn=A et donc:
lim An=A=liminfAn.

Il ne te reste plus qu'a montrer que limsupAn=A et la tu vas devoir te servir de la deuxieme partie de la definition de la limite de An, que tu as oublié de mettre .... .

essaie de traduire ce poste en francais en terme ensembliste(en tachant de comprendre biensur) pour demain et je te dirai si c'est bon. C'est la motié de la demo pour l'inclusion (la reciproque c'est trois lignes et 3 posts avant).

par **barbu23** » 13 Aoû 2007, 07:55

Pour montrer que :

.

Tu as dejà:

:

et

.
Or, on sait que :

et donc :

Il ne te reste plus qu'a montrer que

et la tu vas devoir te servir de la deuxieme partie de la definition de la limite de An, que tu as oublié de mettre ....

.

:lol5:
Mais en réalité, j'ai pas trop compris ce que tu essayes de m'expliquer "BQss",...je ne sais pas pourquoi tu as introduit le symbole "union" au debut, alors qu'on a besoin d'une "intersection" ... !!

par **barbu23** » 13 Aoû 2007, 08:05

Dis moi ce qui ne va pas dans ce raisonnement ..!:

:

Mais je ne suis pas sûr que la dernière implication soit correcte !!

par **barbu23** » 13 Aoû 2007, 08:25

Je m'explique :
la dernière implication provient du fait que :
Pour :

:

et

et .... etc.

n'est ce pas "BQss", est ce que c'est vrai ça ?!

par **BQss** » 13 Aoû 2007, 13:25

BQss a écrit:pour montrer que lim An= A --> limsup=liminf

bonjour, voilà la première moitié de la demo:

on suppose que

tel que

ce qui implique que:

ou plus simplement

or

et donc

donc

Mais par ailleurs on sait que

donc

reste à montrer que

(ce qui se fait avec la même technique, c'est à dire cette fois en montrant que

)

par **barbu23** » 13 Aoû 2007, 15:39

Bonjour :
Merci "BQss" pour ta reponse, je vais tout de suite reflechir à la suite de l'exo ..
Mais j'ai une autre question à vous poser :
Est ce que l'implication suivante est correcte :

et

par **barbu23** » 13 Aoû 2007, 15:43

Je pense que oui :

par **legeniedesalpages** » 13 Aoû 2007, 15:45

,

,

donc

par **BQss** » 13 Aoû 2007, 15:46

barbu23 a écrit:Est ce que l'implication suivante est correcte :
et et

biensur

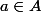
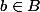
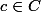
donc

consequence:

ps: on peut s'tutoyer hein, je suis pas ton prof.

par **BQss** » 13 Aoû 2007, 15:51

lol ba voila ...

par **barbu23** » 13 Aoû 2007, 15:54

D'accord !

par **barbu23** » 13 Aoû 2007, 16:01

Alors on a :

:

par **barbu23** » 14 Aoû 2007, 23:32

BQss , tu as écris dans tes messages precedents : "Par ailleurs, on sait que :

" ... tu peux me dire pourquoi ...?!
Merci infiniment !!

par **barbu23** » 15 Aoû 2007, 17:11

Help pls !!
:marteau: :cry:

par **barbu23** » 15 Aoû 2007, 19:54

"alben", "Alexandre le Grand", "anima", "Babe", "DidierK", "emdro", "hams",
"marie49", "Severine_b21", "Skullkid", "sue", "Yorgen" ...
help pls !! :lol2:

par **marie49** » 15 Aoû 2007, 21:35

A est la limite de ta suite d'ensembles. C'est donc une valeur d'adhérence.
Et par définition la liminf est la plus petite valeur d'adhérence, d'où le résultat.

par **barbu23** » 15 Aoû 2007, 23:28

Merci "marie49" pour ta reponse !!!
Mais je ne suis pas sûr que ce soit la bonne methode car la definition de la limite d'une suite d'ensembles ne coincide pas avec celle de la limite d'une suite d'éléments dans un espace topologique ou metrique, pour enfin se permettre de parler de valeur d'adhérence ... c'est vrai n'est ce pas ?
On aurait définit la limite d'une suite d'ensembles comme ça : ( juste pour t'expliquer, je sais que c'est faux )

:

..
Je dis pas que c'est pas juste ce que tu viens de m'expliquer, mais je manque d'explications sur ce point là ...j'aimerai que tu m'expliques pourquoi !!
En tous cas, merci beaucoup pour ta reponse !!!

Suite d'ensembles !

Qui est en ligne