Suite : Somme [preuve]

[allomomo]

Salut tout le monde,

représente la somme des termes consécutifs d'une suite arithmétique.

J'aimerai savoir comment vous feriez pour preuver que :
On commençant par :

.
.
.
donc :
Merci de bien vouloir expliquer les étapes si c'est nécessaire.

Merci,

[Anonyme]

Bonjour,

C'est très facile par récurrence.

Soit la propriété P(n) : "1+...+n=n(n+1)/2"

P(1) est vraie.

Supposons P(n) vraie.
1+...+n+(n+1)=n(n+1)/2 + (n+1) = (n^2 +n +2n +2)/2 = (n+1)(n+2)/2
Donc P(n+1) est vraie.

Donc P(n) est vraie pour tout n entier >= 1.

Nicolas

[Anonyme]

Autre méthode, en écrivant Sn dans les 2 sens :

Sn = 1 + 2 + 3 + ... + n
Sn = n + n-1 + ... + 1
-------------------------
2Sn = (n+1) + (n+1) + ... + (n+1)
2Sn = n.(n+1)

D'où le résultat.

Nicolas

[allomomo]

Merci bcq Nicolas_75,

[phenomene]

Ajoutons que seule la démonstration par récurrence est rigoureuse. L'autre méthode masque une récurrence cachée (par les points de suspension) si l'on veut l'appliquer pour une valeur quelconque de l'entier . On pourrait la rédiger rigoureusement en utilisant la notation et un changement d'indice, mais justifier ce changement d'indice revient à prouver la commutativité de l'addition de entiers, ce qui est certes connu de tous, mais qui, s'il fallait le démontrer, se ferait... par récurrence !

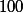
Cette seconde méthode est néanmoins très astucieuse et l'on raconte que Gauss enfant étonna son instituteur en trouvant grâce à elle immédiatement la somme des entiers de à , tandis que ses petits camarades effectuaient les additions une à une...

[Bertrand]

Bonjour

Je profite du sujet d' allomomo pour vous demander une bricole sur les suites numériques.

J'aimerai connaître vos commandes en matière de graph sur les calculettes TI.
Lorsque que je veux voir l'allure d'une suite j'ai systématiquement un rendu erroné. Je vais vous donner l'exemple d'une suite: (2+3Un)/(4+Un)=U(n+1)
Pouvez-vous me dire la méthode pour la visualiser sur graphique. Merci d'avance.