Tribus
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 23 Juin 2007, 17:13
par legeniedesalpages » 23 Juin 2007, 17:13
Bonjour,
je ne vois pas comment montrer que la tribu Borélienne
)
est incluse dans la tribu engendrée par
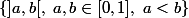
.
Merci pour votre aide.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 23 Juin 2007, 17:32
par aviateurpilot » 23 Juin 2007, 17:32
c'est quoi
)
??
 par legeniedesalpages » 23 Juin 2007, 17:50
par legeniedesalpages » 23 Juin 2007, 17:50
)
est la tribu engendrée par les ouverts de [0,1].
-
tbotw69
- Membre Relatif
- Messages: 122
- Enregistré le: 06 Nov 2005, 12:12
-
 par tbotw69 » 23 Juin 2007, 18:10
par tbotw69 » 23 Juin 2007, 18:10
Tu pourrais pas utiliser cette propritété : si la topologie de T est engendrée par une famille dénombrable A, stable par intersection finie, la tribu borélienne associée à T est aussi engendrée par A. (T est un espace topologique)
-
tbotw69
- Membre Relatif
- Messages: 122
- Enregistré le: 06 Nov 2005, 12:12
-
 par tbotw69 » 23 Juin 2007, 18:11
par tbotw69 » 23 Juin 2007, 18:11
Euh, non, désolé, j'y suis pas du tout :mur: :mur:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 23 Juin 2007, 18:14
par fahr451 » 23 Juin 2007, 18:14
bonsoir
un ouvert de R est réunion DENOMBRABLE d'intervalles ouverts
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 23 Juin 2007, 18:21
par aviateurpilot » 23 Juin 2007, 18:21
legeniedesalpages a écrit:)
est la tribu engendrée par les ouverts de [0,1].
si j'ai bien compris ce que tu dit là.
)
est la tribu engendrée par
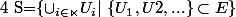
avec
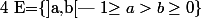
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 23 Juin 2007, 18:56
par fahr451 » 23 Juin 2007, 18:56
sur U ouvert non vide on définit R une relation binaire
xRy ssi il existe ]a,b[ inclus dans U contenant x et y
R est une relation d'équivalence
on montre que les classes sont des intervalles ouverts
1) intervalle car convexe
2) ouvert
donc U est réunion d'intervalles ouverts DISJOINTS non vides ]ai,bi[ i dans I
la réunion est alors dénombrable ( au plus)
car on peut choisir un rationnel qi ds chaque intervalle et donc construire une application INJECTIVE de I dans Q
i-> qi
donc tout ouvert est dans la tribu T engendrée par les intervalles ouverts et donc la tribu borélienne qui est par définition la plus petite tribu contenant les ouverts est incluse dans la tribu T
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités