équation avec sinus et cosinus

[juli]

Bonjour,

dans un exercice j'obtiens
cos (2x+pi/3) = cos (pi/4-x)

Je veux résoudre cette équation dans R puis dans [0;2pi]. Je ne vois pas comment faire.

Pour résoudre dans R j'ai dit :
cos a = cos b donc a=b
2x+pi/3= pi/4-x
en résolvant j'ai x= -pi/36

Mais cela ne me semble pas correct.
Merci de m'éclairer.

[fonfon]

salut,

rappel:
ou

apres il faut que tu regarde les solutions qui conviennent en t'appuyant sur ton cercle trigo.

[juli]

Merci, donc si j'ai bien compris on a dans R

x = 23pi/36 ou x = 17pi/12

cela me semble bizard comme résultat tout de même ... ?

[amine801]

slt
pour x = 17pi/12 c bon
pour l'autre reverifie te calcul :we:

[juli]

Mais comment trouver sur le cercle l'emplacement de 17pi/12 ?

[amine801]

et l'autre solution tu la trouve? :we:
pour ce qui est du cercle on peux dire que 17pi/12 c'est entre
pi et 3pi/2

[juli]

2x + x = pi/4 - pi/3 + 2pi
3x = 3pi/12 - 4pi/12 + 24pi/12
3x= 27pi/12 - 4pi/12
3x = 23pi/12
x = 23pi/12 * 1/3
x = 23pi/36 !?

[amine801]

oui oui c bon
donc c tout c'est fini
S={23pi/36,17pi/12}

[juli]

C'est fini pour R, maintenant me reste à trouver l'intervalle [O;2pi]
Merci pour ton aide

[amine801]

non ca c'etait la solution pour [0,2pi]
pour R il faut garde le k dans l'expression ca fait une infinite de solution

[juli]

J'aurai dit

- dans R : S= 23pi/36 ou 17pi/12

- dans [0;2pi[ S= {pi/2; -pi/4}
en effet
pi < 17pi/12 < pi+pi/2 et
pi/3 < 23pi/6 < pi - pi/3

[juli]

J'aurai dit :

- dans R : S= 23pi/36 ou 17pi/12

- dans [0;2pi[ S= {pi/2; -pi/4}
en effet
pi < 17pi/12 < pi+pi/2 et
pi/3 < 23pi/6 < pi - pi/3

[amine801]

voila dans R c'est

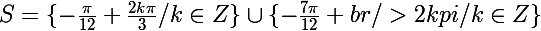
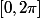
pour il faut choisir les bons k pour rester dans l'intervalle
voila

[juli]

Merci beaucoup !

[amine801]

ah au faite je pense que tu la remarquer sur

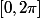
il ya plus de deux solutions

[juli]

Oui :
7pi/12 ; 15pi:12 ; 23pi/12

[amine801]

:++: ok c bon :we: