Intégrale fonction ln
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
par Joker62 » 29 Jan 2007, 19:41
Pas très joli en effet lol
-
mathelot
par mathelot » 30 Jan 2007, 08:25
bonjour,
en suivant les indications de fahr, je trouve que l'intégrale vaut:
- \int_{1}^{1+\sqrt{2}} \quad \frac{ \left( x^4 - 2 x^2 +1 \right) \left(x^2+x+1 \right) }{x^2 \left( x^4+2x^3-2x^2+2x+1 \right)} \quad dx)
avec:
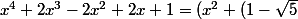x+1)(x^2+(1+\sqrt{5})x+1))
-
mathelot
par mathelot » 31 Jan 2007, 10:14
-
mathelot
par mathelot » 31 Jan 2007, 16:02
quelques calculs plus tard, j'obtiens une expression relativement simple (plus simple que MAPLE):
---------------------------------------------------------------
-
mathelot
par mathelot » 01 Fév 2007, 12:35
Bon, après quelques heures (quelques jours ?) , j'ai pu obtenir la valeur exacte et agréable (ce post annule le précédent):
soient:
 dx = 2 \ln (\psi) - 2 + 2 \sqrt {\phi -1} \quad \arctan \left( \frac{ \left( \phi + 1 \right) \sqrt{ \phi - 1} }{\psi} \right) - \phi \sqrt{\phi -1} \quad \ln \left( \frac{ \psi (3 \phi + 2 ) + 2 \phi + 1 + \sqrt{ \phi} \psi \left( 1+\phi \right) }{\psi \left( 3 \phi + 2 \right) + \phi +1 } \right))
(vérifié à l'aide Maple)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
