Intégrale fonction ln

par **d.masse3** » 29 Jan 2007, 10:19

bonjour
je coince un peu sur l'intégrale suivante :

integrale de 0 à 1 de ln(x^2 +sqrt(x^2+1))

meme en passant par le sinus hyperbolique je ne vois pas...

merci de votre aide.

par **manu18ck** » 29 Jan 2007, 10:30

essaie un changement de variable je l'ai pas fait mais ca peut peut etre marcher

par **andros06** » 29 Jan 2007, 10:43

tu veux primitiver argsh(x) , je te conseille de visiter le lien suivant : ça te donnera peut-être des idées.
http://fr.wikipedia.org/wiki/Primitives_de_fonctions_hyperboliques_r%C3%A9ciproques

Sinon t'as essayé une IPP ? Intégrer 1 et dériver argsh(x) par exemple ...

par **d.masse3** » 29 Jan 2007, 10:58

le probleme c'est que x est au "carré" donc ce n'est pas l'intégrale de argsh

par **andros06** » 29 Jan 2007, 10:59

scusi ! pas fait gaffe
par contre ma question sur l'IPP reste valable .

par **d.masse3** » 29 Jan 2007, 11:05

L 'IPP ... c'est pire encore.

par **fahr451** » 29 Jan 2007, 11:33

pas de difficulté théorique

1)IPP -> fraction rationnelle en x et racine ( x^2+1)
2) changement de variables x = sh t -> fraction rationnelle en ch et sh
3) changement de variables u = exp (t) -> fraction rationnelle en u
4) décomposition en éléments simples
5) intégration terme à terme

bon calcul ...

par **d.masse3** » 29 Jan 2007, 11:42

ha oui quand meme...cela fait pas mal d'étapes.

merci beaucoup à tous, je me lancerais dans le calcul en soirée, vous tiendrais au courant du résultat ...ou des difficultés.

par **amine801** » 29 Jan 2007, 12:29

Je suis en informatique et modélisation mathématique et justement je travaille sur un projet qui a pour but
De créer un programme qui calcul nimporte quelle intégreral ma version est presque final
Jai fait le test pour ta fonction et ca ne marche pas
Je pense quil nexiste pas de fonction qui puisse exprimer cette primitive
Cela dit si tu trouve une solution sa serai sympa de me tenir au courant

par **d.masse3** » 29 Jan 2007, 12:41

1)IPP -> fraction rationnelle en x et racine ( x^2+1)
2) changement de variables x = sh t -> fraction rationnelle en ch et sh
3 changement de variables u = exp (t) -> fraction rationnelle en u
4) décomposition en éléments simples
5) intégration terme à terme

fraction rationnelle en u du type

(u^8+ u^7+u^5+u^3+u+1)du/ u^8+u^7+u^6+2u^5+u^4+u^3+u^2 ??

j'avoue je cale...

par **fahr451** » 29 Jan 2007, 12:44

amine c'est obligé que ça marche

d'autre part j'ai un peu (pas beaucoup) regardé Li2 on peut vraiment calculer Li2(-2)? et Li2(-3)? si oui peux tu me donner la solution s'il te plait ?

par **fahr451** » 29 Jan 2007, 12:47

d masse tu cales parceque tu ne sais pas décomposer la fraction en éléments simples ( factorisation du dénominateur ) (moi non plus d 'ailleurs) mais d'un point de vue théorique
c'est fini

.ca devrait être de degré 5 au dénominateur

par **amine801** » 29 Jan 2007, 13:06

mon programme aussi il cale apparemment il suis le même cheminement après il narrive pas a trouver la solution :cry:
pour les polylogarithmes je mettrais la réponse des que possible (les calcules sont un peu delicas)

par **andros06** » 29 Jan 2007, 14:04

MAPLE retourne une primitive ya du argch, du arctan et du ln de racine. C'est un peu horrible. Bonne chance à toi d.masse3 ...

par **amine801** » 29 Jan 2007, 14:07

stp tu peux me filer une capture d'ecran de maple

par **mathelot** » 29 Jan 2007, 14:23

le polynome au dénominateur a des coefficients symétriques par rapport à celui du milieu, ce qui divise le degré de l'équation par 2:
d'où:

en posant

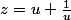
on revient à une équation de degré 3. Avec un peu de chance, celle-ci a une racine évidente...
PS: elle a une racine évidente z=0 et le dénominateur admet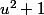

(entre autres) comme facteur.
pour calculer les autres racines,il suffit de résoudre:

(racines évidente !!)
puis

donc le dénominateur se factorise bien, finalement...

par **andros06** » 29 Jan 2007, 14:47

Amine,
file moi ton adresse mail et je t'envoie le fichier en pdf.

par **amine801** » 29 Jan 2007, 14:51

voila c'est fait en MP

par **amine801** » 29 Jan 2007, 15:46

merci andros:

par **andros06** » 29 Jan 2007, 15:47

Voilà la primitive...

Intégrale fonction ln

intégrale fonction ln

Qui est en ligne