Problème avec les nombres dérivés

par **ninon** » 07 Jan 2007, 14:18

bonjour,
j'ai besoin de vos conseils pour mon exercice car je l'avoue je suis un peu perdu

on désire fabriquer une cuve en tôle ayant la forme d'un parallélépipède rectancle de base carrée. on note x la longueur d'un coté de la base et h la hauteur de la cuve
pour la commodité de fabrication on doit avoir x compris entre 0.5 et 3.4, on néglige l'épaisseur de la tôle

1. le volume de la cuve est 1mcube
a.calculer la surface totale de la cuve en fonction de x et h . en déduire h en fonction de x

b.vérifier que la surface totale de la cuve S ( les 6 faces) est définie par S(x)=g(x) ( g (x) = 2xcarré+4/x )
lorsque x compris [ 0.5 ; 3.4]

c. en déduire les dimensions de la cuve pour utiliser le moins possible de métal . quelle est alors la forme de la cuve ?

voila alors si quelques âmes charitables pouvaient m'expliquer un peu ce qu'on attend de moi
merci beaucoup

par **ninon** » 07 Jan 2007, 18:59

personne peut me conseiller , me donner quelques pistes?

par **maturin** » 08 Jan 2007, 14:54

1a je pense qu'on te demande le volume et non la surface (la surface c'est la question d'après).
Il te faut donc calculer le volume d'un cylindre de base carré et de hauteur h.

C'est pas très dur comme question si tu sais pas tu tapes sous google "volume+cylindre" il devrait te donner la formule.

b) la surface dela cuve c'est la surface de tole nécéssaire.
c'est à dire surface des 4 côtés + surface du fond + surface du couvercle
(ils te précisent qu'il y a 6 faces dans la question d'après donc il doit bien y avoir un couvercle).
t'as des rectangles sur les côtés et des carrés au fond et dessus, tu devrais y arriver.

c) là c'est une étude de fonction. Il faut trouver le minimum de lafonction S(x)

par **ninon** » 08 Jan 2007, 16:09

1. a. j'ai vérifier c'est bien la surface quon demande

pour la b. d'accord mais par contre pr la c. il faut que je calcul le nombre dérivée?

merci

par **maturin** » 08 Jan 2007, 16:36

alors pour la 1 c'est le volume qu'il te faut sinon tu peux aps répondre à la question c.
Il y a une erreur d'énoncé c'est assez fréquant dans les bouqins.
donc volume=aire de la base*hauteur=1 ça te donne h en focntion de x.

Tu remplaces h par sa valeur en fonction de x dans l'équation de la surface et tu trouves la 2).

pour la 3) oui il faut que tu dérives, tu fais un tableau de variation et tu trouveras le mini quand la dérivée sera nulle.

par **ninon** » 08 Jan 2007, 16:46

d'accord je comprend mieux la seul chose c'est que je vois pas comment on trouve h en fonction de x h = racine carré de xcarré c'est possible?

par **ninon** » 08 Jan 2007, 16:58

a non j'ai dis une bêtise
v= x * h donc 1= x * h donc h= 1/X

est ce que tu peux confirmer?

par **maturin** » 08 Jan 2007, 17:03

non c'est pas ça non plus mais tu t'en approches :)
l'aire de la base c'est l'aire d'un carré de côté x.
La hauteur c'est h
donc v= ?

par **ninon** » 08 Jan 2007, 17:24

v = xcarré * h ?

par **maturin** » 08 Jan 2007, 17:26

oui et v=1 donc h=1/(x²)

par **ninon** » 08 Jan 2007, 17:44

génial !
aller encore une tite question : on veut utiliser 24 mcarré de tôle pr la construction 1. calculer la surface totale de la cuve en fonction x et h

alors s = 24 donc x * h =24 et h= 24/x ?

par **maturin** » 08 Jan 2007, 18:06

tu as déjà calculé la surface normalement et c'est pas x*h...

Avant de remplacer h par sa valeur tu devais avoir:
S=4hx+2x² (ce qui correspond aux 4 côté rectangles x*h + les 2 côtés carrés inférieur et supérieur x²)

donc 4hx+2x²=24

par **ninon** » 08 Jan 2007, 19:13

oo la grosse betise que j'ai pas dite... :dodo:

et ba merci bien maturin

ps: jcrois bien que je vais bientot revenir faire apelle a toi :happy2:

par **ninon** » 10 Jan 2007, 14:32

bonjour,
j'ai encore quelques questions ,

b. vérifier que le volume V de la cuve est V (x)=f (x) ( (f (x) = xcube -3xcarré+ 35/12x + 1/12)

dans les questions précédentes on a déja calculé le volume et je comprends pas comment on pourrait s'approcher de f (x)

c. en déduire les dimensions de la cuve pr que le volume soit maximal

d. déterminer la valeur de x, à 10 exposant -1près pr que le volume soit de 2mcube

encore perdue :triste:

merci

par **maturin** » 10 Jan 2007, 16:38

b. on a effectivement déjà vu que v=h*x²
et là tu as de plus 4hx+2x²=24
il te faut donc calculer h en fonction de x puis remplacer h dans l'expression du volume.

Attention dans la premiere partie du problème on supposait que le volume était de 1 et donc que h=1/x². Ce n'est plus le cas maintenant !

c. pareil il te faut faire une étude de fonction de v(x) en calculant v'(x), en cherchant le signe de v'(x), en tracant les variations de v et donc en déduire le max.

d. là tu traces la courbes approximativement et tu regardes pour quelle valeur de x tu as v(x)=2 (il te faut une valeur de x à 0.1 près)

par **ninon** » 10 Jan 2007, 18:06

oui pr la b. j'ai trouve h=24/4x+ 2xcarré , simplié ca donne h= 24+2xcarré*4x le tt sur 4x dc h=24 + xcarré c'est possible?

ca donnerait v=xcarré *h
v= xcarré * (24 + xcarré)

MERCI pr la c. et la d.

par **maturin** » 10 Jan 2007, 18:44

ouhlala que c'est horrible ce que tu écris...
4hx+2x²=24
=> 4hx=24-2x² (et non pas +)
=>

(attention à bien tout diviser)
=>

par **maturin** » 10 Jan 2007, 18:57

sinon il y a une subtilité a laquelle il faut penser (t'en aura besoin pour la question d afin de n'avoir qu'une solution et à la question c pour limiter ton ensemble de définition) :
La largeur et la hauteur doivent être positive car ce sont des longueurs.

Donc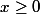

et

implique

ce qui revient à dire que si x dépsse cette valeur la surface de ton carré du dessous+du dessus de la cuve va dépasser 24.

Donc l'ensemble de définition de tes fonctions est

Problème avec les nombres dérivés

problème avec les nombres dérivés

personne?

Qui est en ligne