Les intégrales

[AMARI]

Bonjour à TOUS,
On nous donnes l'intégrale suivante de (1 à e )

Wn =ʃ (Lnx)^n.dx
On nous demandes de prouver que :
Wn = e - nW(n-1)
On prenant : U'= 1 U= x
V= (Lnx)^n V'= n(Lnx)^(n-1)
Avec ʃU'V = (UV) - ʃUV'

On trouve à la fin que :
Wn = e - nx(Lnx)^(n-1) (Avec un "x" en plus)
Comment le supprimer ?

Je vous Remercie Vivement

[catamat]

Bonjour

Le problème c'est la dérivée de v
v est du type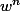 sa dérivée est
Tu as oublié w'...

[AMARI]

Bonjour catamat,

Mais j'ai donné la dérivé de "V" qui est :
V'= n(Lnx)^(n-1)
et on trouve à la fin que :
Wn = e - nx(Lnx)^(n-1) (Avec un "x" en plus)
Comment le supprimer ?

Merci catamat

[Pisigma]

Bonjour,
comme déjà dit par catamat il te manque la dérivée de dans

[catamat]

Je sais que tu as écrit V'(x) le problème c'est que c'est faux !!

Il manque la dérivée de w qui est w'(x)=1/x

[AMARI]

Bonjour à catamat et Pisigma,

Et oui, j'ai oublié que : (U^n)' = nU^(n-1).U'

((Lnx)^n)' = n(Lnx)^(n-1).(1/x)

Un Grand Merci à Vous de ma Part