BON SOIR
lim┬(-∞)〖(sin(πf(x)-2f(x))/(cos(1/x)-1)〗 avec f(x) =x +√(x^2+|x| )
ANALYSE
10 messages
- Page 1 sur 1
Re: ANALYSE
Salut,
Il faudrait que tu te mette au MimeTeXpour que ce soit plus facilement lisible.
-2f(x)\big)}{\cos\big(\frac{1}{x}\big)-1}\ \ \mbox{ o\`u }\ \ f(x)=x+\sqrt{x^2+|x|})
C'est bien ça ton énoncé ?
Si oui, lorsque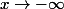 , en utilisant le conjugué, on voit que
, en utilisant le conjugué, on voit que ) tend vers
tend vers  donc le numérateur tend
donc le numérateur tend \!\not=\!0) alors que le dénominateur tend vers 0.
alors que le dénominateur tend vers 0.
Donc je soupçonne que ce n'est pas ça le vrai énoncé . . . (mais comme ton parenthésage est défaillant c'est pas étonnant que je me goure d'interprétation)
Il faudrait que tu te mette au MimeTeXpour que ce soit plus facilement lisible.
C'est bien ça ton énoncé ?
Si oui, lorsque
Donc je soupçonne que ce n'est pas ça le vrai énoncé . . . (mais comme ton parenthésage est défaillant c'est pas étonnant que je me goure d'interprétation)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: ANALYSE
Pour
Donc ta grosse fraction est équivalente à
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: ANALYSE
Bonjour
Pour la limite de f c'est assez classique en terminale pour le reste c'est bien plus technique ...
Pour f il suffit d'utiliser l'expression conjuguée et une factorisation :
=x+\sqrt{x^2+|x|}=\dfrac{(x+\sqrt{x^2+|x|})(x-\sqrt{x^2+|x|})}{x-\sqrt{x^2+|x|}})

Or x tend vers , donc |x|=-x
, donc |x|=-x
donc
=\dfrac{x}{x-\sqrt{x^2-x}}=\dfrac{x}{x-\sqrt{x^2(1-\dfrac{1}{x})}}=\dfrac{x}{x-|x|\sqrt{1-\dfrac{1}{x}}}=\dfrac{x}{x+x\sqrt{1-\dfrac{1}{x}}}=\dfrac{1}{1+\sqrt{1-\dfrac{1}{x}}})
ce qui donne bien la valeur de la limite en soit 0,5.
soit 0,5.
Pour la limite de f c'est assez classique en terminale pour le reste c'est bien plus technique ...
Pour f il suffit d'utiliser l'expression conjuguée et une factorisation :
Or x tend vers
donc
ce qui donne bien la valeur de la limite en
Re: ANALYSE
Sinon, niveau terminale, c'est jouable, vu qu'au numérateur on n'a besoin que du D.L. à l'ordre 1 qui s'obtient dés qu'on sait dériver des fonctions.
Et pour le cosinus du dénominateur, je pense qu'en terminale ils ont vu que :
}{h}=\lim_{h\to 0}\dfrac{\sin(h)-\sin(0)}{h-0}=\sin'(0)=\cos(0)=1)
Voire sans doute aussi que :
}{h^2}=\lim_{h\to 0}\dfrac{1-\cos^2(h)}{h^2\big(1+\cos(h)\big)}=\lim_{h\to 0}\Big(\dfrac{\sin(h)}{h}\Big)^2\times\dfrac{1}{1+\cos(h)}=1^2\times\dfrac{1}{1+1}=\dfrac{1}{2})
Mais ça c'est même pas utile ici si on veut juste la limite et pas un équivalent vu qu'il suffit de savoir que}{h}=0) qui s'obtient par simple définition de la dérivée.
qui s'obtient par simple définition de la dérivée.
Bref, c'est faisable, mais bien compliqué vu que pour le numérateur, il faut non seulement calculer la limite de) en -oo (en faisant par exemple comme le fait catamat), mais il faut aussi calculer la limite de
en -oo (en faisant par exemple comme le fait catamat), mais il faut aussi calculer la limite de -\frac{1}{2}\big)) pour conclure (ça peut aussi se calculer uniquement en utilisant des quantités conjuguées, mais c'est bien chiant . . . )
pour conclure (ça peut aussi se calculer uniquement en utilisant des quantités conjuguées, mais c'est bien chiant . . . )
Et pour le cosinus du dénominateur, je pense qu'en terminale ils ont vu que :
Voire sans doute aussi que :
Mais ça c'est même pas utile ici si on veut juste la limite et pas un équivalent vu qu'il suffit de savoir que
Bref, c'est faisable, mais bien compliqué vu que pour le numérateur, il faut non seulement calculer la limite de
Modifié en dernier par Ben314 le 04 Nov 2023, 18:54, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: ANALYSE
Bon si on détaille le calcul de Ben (si j'ai bien compris le truc...) on a ceci :
On peut écrire la fonction sous la forme suivante :
-2f(x)}{f(x)-\frac{1}{2}}\times\dfrac{f(x)-\frac{1}{2}}{\frac{1}{x}}\times\dfrac{\frac{1}{x}}{\cos\big(\frac{1}{x}\big)-1}=A\times B\times C)
On a avec h qui tend vers 0 par valeur négatives, donc 1/C a pour limite 0 et 1/C>0 car les deux termes de la fraction sont négatifs.
avec h qui tend vers 0 par valeur négatives, donc 1/C a pour limite 0 et 1/C>0 car les deux termes de la fraction sont négatifs.
Donc C a pour limite
A peut s'écrire ou encore
ou encore -g(\frac{1}{2})}{t-\frac{1}{2}}) où
où =\sin\pi t-2t) avec t qui tend vers
avec t qui tend vers 
La limite de A est donc) c'est à dire -2.
c'est à dire -2.
Reste la limite de B...
-\frac{1}{2})=) ou en reprenant l'expression de f(x) obtenue dans mon message précédent :
ou en reprenant l'expression de f(x) obtenue dans mon message précédent :
=\frac{x}{2}\big(\frac{2-1-\sqrt{1-\frac{1}{x}}}{1+\sqrt{1-\frac{1}{x}}}\big)=\frac{x}{2}\big(\frac{1-\sqrt{1-\frac{1}{x}}}{1+\sqrt{1-\frac{1}{x}}}\big))
C'est là que l'expression conjuguée va servir, on obtient :
^2}\big)=\frac{\frac{1}{2}}{(1+\sqrt{1-\frac{1}{x}})^2})
Donc la limite de B en est
est 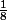
Finalement ABC a pour limite
On peut écrire la fonction sous la forme suivante :
On a
Donc C a pour limite
A peut s'écrire
La limite de A est donc
Reste la limite de B...
C'est là que l'expression conjuguée va servir, on obtient :
Donc la limite de B en
Finalement ABC a pour limite
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
