Exercice d analyse 1s

[nour2013]

merci bien
j ai trouvé une solution trés simple
en élèvent l inégalité au carré 0<=g(x)<=f(x)<=h(x)
on calcul f²(x)-g²(x) et h²(x)-f²(x) et j ai vérifié avec géogebra


enfin
merci bien amicalement

[zygomatique]

n'est-ce pas ce que je te proposais dès mon premier post ? ....

:mur:

[paquito]

[quote="nour2013"]merci bien
j ai trouvé une solution trés simple
en élèvent l inégalité au carré 0=0 en étudiant la fonction f-g est intéressante, mais ici les calculs masquent tout son intérêt; donc autant faire comme toi.

Mis à part le calcul pénible f²(x)-g²(x) donne x^3(-0,25x) ce qui ne pose aucun problème; pour h²(x)-g²(x), on obtient (x^3/13)(9x^3-12x²+28x+32) et il faut étudier les variations du polynôme de degré trois pour avoir son signe; après il faut résoudre -x²+4x+4=4,00039999; ça tombe juste, mais on à utilisé la touche racine carrée de la calculatrice pour trouver x=10^-4; donc encadrer V(4,0003999) est stupide et tout le monde s'en fout ; en plus ça quoi! on obtient:

2,000099995=< V4,00039999=<2, 000099995008.

Calcul qu'on fait tous les jours! :ptdr:

[nour2013]

merci beaucoup cher professeur
j ai refait les calculs je crois qu il y a une faute au niveau de l expression du polynôme
j ai trouvé (-3x^3+8x²+20x-16)

h²(x)-f²(x)= x^3 (-3x^3+8x²+20x-16)/16

est il possible de m étudier le signe de polynôme

merci bien

[paquito]

J'ai dû faire des fautes de frappe! si , alors; (j'ai fait le calcul à la main et géogébra a confirmé);
donc on retombe sur du second degré, ce qui va tout seul (Delta>0); en fait, j'avais du prendre à la place de .

Donc, ça y est; on est arrivé à bout de cet exercice passionnant :censure:

Ce qui est quand même surprenant, c'est qu'on utilise la touche racine carrée pour trouver une approximation d'une racine carrée; j'ai du mal à comprendre la logique...

[zygomatique]

pourquoi un discriminant ? (d'ailleurs faux car < 0)

puisque

:zen:

[Shew]

j aime bien
avoir une réponse détailler surtout la 2 em question

On considère les fonctions f, g et h définies sur [0,2]
Par f(x)= racine(-x²+4x+4) , g(x)=2+x-1/2 x² , h(x)= 2+x- 1/2 x²+ 1/4 x^3
On désigne par Cf ,Cg et Ch leurs courbes représentatives dans un repère (o,i,j)
1-Etudier chacune des fonctions f,g,h
2- Montrer que g(x) <= f(x) <=h(x) ,x de [0,2] ( <= inférieur ou égale)
3-Tracer Cf ,Cg et Ch
4-Déterminer une valeur approché à (10)-12 prés de racine(4,00039999)

merci bien amicalement

Pour trinome du second degrés, discriminant, on se rappel qu'un nombre et sa racine carré ont le même sens de variation .

[Shew]

, on trouve .

On prouve que c'est positif sur [0;1] et donc sur [0;2], par conséquent sur [0; 2] d(x) est croissante et comme d(0) =0, on a d(x)>=0 et donc F(x)>=g(x)/ Ouf!!

Euh oui .... mais non , en tout cas pas sur l'intervalle donné [0; 2]. Pour x = 2 on a donc d est bien positive sur [0; 1] mais pas sur ]1; 2] .

[paquito]

Bonjour,

je suis passé aux carrés que pour , le problème étant évident pour , donc ce qui est écrit l'est sous la condition .

[Shew]

Bonjour,

je suis passé aux carrés que pour , le problème étant évident pour , donc ce qui est écrit l'est sous la condition .

Bonjour

Le problème etant que la démonstration doit se faire dans l'intervalle [0; 2] j'en viens d'ailleurs à me demander après votre développement si est vraiment vérifiable sur cet intervalle .

[zygomatique]

:cry:

si a et b sont positifs alors comparer a et b est équivalent à comparer a^2 et b^2 ...

et il est inutile de distinguer x < 1 ou x > 1 ....

[Ingrid55]

Oui , mais il faut déjà savoir si a > b , non ?

Mais bon , dans cet exercice , l'inégalité est déjà posée donc pas de soucis , il faut juste élever au carré pour démontrer (comme ceci a été dit dans un des posts précédents ) .

[zygomatique]

quand on veut comparer deux nombres c'est qu'on ne sait pas quel est le plus grand ....

[Shew]

:cry:

si a et b sont positifs alors comparer a et b est équivalent à comparer a^2 et b^2 ...

et il est inutile de distinguer x 1 ....

Peut être pour et mais ne sera certainement pas positif pour toutes les valeurs dans ces conditions .

Rectification il le sera sur [0; 2] .

[Ingrid55]

Ok! Donc l'intervalle est là pour déduire ....^^!
Il n'y pas un relation direct , mais çà me rappelle le théorème des gendarmes où l'on peut en démontrant : arriver à restreindre une intervalle .

[Shew]

Le problème c'est qu'on ne sait pas si et

la forme réduite ne nous apprend rien . On a or même si on sait que sera toujours positif, généralement dans le cas de on cherchera à le démontrer et donc utiliser ses racines .

[paquito]

On avait comme problème: à prouver sur 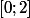; sur ]1; 2], le 1° membre est positif et le deuxième négatif; donc c'est vérifié sur ]1; 2], pa r compte sur [0; 1] les deux membres sont positifs ce qui a conduit à comparer les carrés vu l'allure de l'expression de gauche ce qui à conduit à qui dépendait finalement de dont des racines étaient extérieures à [0; 1].

Conclusion: l'inégalité est trivialement vérifiée sur ]1; 2], on a prouvé qu'elle était vérifié sur [0; 1], donc elle est vraie sur [0; 2].

rmq: c'est exercice était particulièrement pénible! Le but étaient de trouver à près!!

[zygomatique]

On avait comme problème: à prouver sur ; sur ]1; 2], le 1° membre est positif et le deuxième négatif; donc c'est vérifié sur ]1; 2], pa r compte sur [0; 1] les deux membres sont positifs ce qui a conduit à comparer les carrés vu l'allure de l'expression de gauche ce qui à conduit à qui dépendait finalement de dont des racines étaient extérieures à [0; 1].

Conclusion: l'inégalité est trivialement vérifiée sur ]1; 2], on a prouvé qu'elle était vérifié sur [0; 1], donc elle est vraie sur [0; 2].

rmq: c'est exercice était particulièrement pénible! Le but étaient de trouver à près!!

non ce problème est pénible uniquement quand on travaille comme une machine ....

une fois qu'on a prouvé que f, g et h sont positives sur [0, 2] il suffit de travailler avec les carrés convenablement comme je l'ai montré avec f et g

pour ce qui est de f et h c'est à peine plus compliqué mais guère plus si on pense les calculs et ce que l'on veut en faire ....

:lol3:

[paquito]

non ce problème est pénible uniquement quand on travaille comme une machine ....

une fois qu'on a prouvé que f, g et h sont positives sur [0, 2] il suffit de travailler avec les carrés convenablement comme je l'ai montré avec f et g

pour ce qui est de f et h c'est à peine plus compliqué mais guère plus si on pense les calculs et ce que l'on veut en faire ....

:lol3:

En fait au départ, j'ai pensé qu'en passant par la dérivée de f-g, ça serait peut être plus simple, mais ici, ça a plutôt compliqué les choses, pour l'autre inégalité, en comparant les carrés, ça a été bien plus rapide; mauvaise intuition.

[Shew]

En fait au départ, j'ai pensé qu'en passant par la dérivée de f-g, ça serait peut être plus simple, mais ici, ça a plutôt compliqué les choses, pour l'autre inégalité, en comparant les carrés, ça a été bien plus rapide; mauvaise intuition.

En elevant au carré f et g sans en passer par la dérivée on se retrouve avec ce qui après simplification n'ait guère mieux pour démontrer l'inégalité . Peut être faut il prendre l'enoncé dans son ensemble et se cantonner à l'encadrement