Bonjour,
Je vous ecris car je bloque sur une question
ENONCE : Une suite est definie par : ∀n∊R, Un⁺1= aUn ₊ b
Suite auxiliaire (Vn) est definit par : ∀n∊ℕ, Vn= Un⁺λ
QUESTION :Montrer que : ∀n∊ℕ, Vn+1= aVn + [(1₋a) λ+b]
Dm Suite terminale (suite auxiliaire)
8 messages
- Page 1 sur 1
Re: Dm Suite terminale (suite auxiliaire)
Bonjour,
Pour être sûr d'avoir bien lu :
La suite) vérifie
vérifie
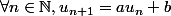
où et
et  sont deux constantes (la suite n'est pas définie, puisqu'on ne connaît pas le terme initial).
sont deux constantes (la suite n'est pas définie, puisqu'on ne connaît pas le terme initial).
Soit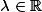 ; on définit la suite
; on définit la suite ) par
par
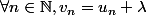
[EDIT : j'ai retiré la multiplication par que j'avais ajouté à tort]
que j'avais ajouté à tort]
Est-ce bien cela ?
Pour montrer que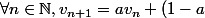\lambda+b)
Qu'as-tu essayé de faire ?
Pour être sûr d'avoir bien lu :
La suite
où
Soit
[EDIT : j'ai retiré la multiplication par
Est-ce bien cela ?
Pour montrer que
Qu'as-tu essayé de faire ?
Modifié en dernier par hdci le 02 Nov 2023, 13:58, modifié 1 fois.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Dm Suite terminale (suite auxiliaire)
Bonjour,
Oui c'est bien ça.
Sincèrement j'ai fait quelque tentatives hasardeuse. Je me suis dis que Vn+1 ressemblait au terme général d'une suite arithmétique Un = Up (n-p) r.
Après je comprends comment trouver le aVn ou encore (1-a).
Et je me dis aussi que ça doit pas être ça vu que ce n'est pas une suite arithmétique
Oui c'est bien ça.
Sincèrement j'ai fait quelque tentatives hasardeuse. Je me suis dis que Vn+1 ressemblait au terme général d'une suite arithmétique Un = Up (n-p) r.
Après je comprends comment trouver le aVn ou encore (1-a).
Et je me dis aussi que ça doit pas être ça vu que ce n'est pas une suite arithmétique
Re: Dm Suite terminale (suite auxiliaire)
Avec
Utilise alors la propriété de
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Dm Suite terminale (suite auxiliaire)
Merci pour votre réponse. Je comprends déja un peu mieux
Donc si j'ai bien compris :
Vn+1 = Un+1 + λ
donc Vn+1 = aUn+1 + b + λ
Vn+1 = a( aUn+ b ) + b
Vn+1 = aVn + b
Est ce bon pour le moment ?
Et dois je utiliser la formule Un = Up (a-p) r ?
Donc si j'ai bien compris :
Vn+1 = Un+1 + λ
donc Vn+1 = aUn+1 + b + λ
Vn+1 = a( aUn+ b ) + b
Vn+1 = aVn + b
Est ce bon pour le moment ?
Et dois je utiliser la formule Un = Up (a-p) r ?
Re: Dm Suite terminale (suite auxiliaire)
inesrMaths a écrit:Vn+1 = Un+1 + λ
donc Vn+1 = aUn+1 + b + λ
Vn+1 = a( aUn+ b ) + b
Il y a une erreur sur la seconde ligne : tu as remplacé
Il y a une erreur sur la troisième ligne : où est passé
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Dm Suite terminale (suite auxiliaire)
D'accord merci beaucoup ! Je commence enfin a comprendre
donc si je reformule : Vn = Un + λ
donc Vn+1 = Un+1 + λ
= aUn + b + λ
= aVn + b + λ
En utilisant la formule Un = Up (n-p) r
Je trouve : Vn+1 = aVn [(n-p) b + λ ]
J'ai enfin compris (grâce a vous) d'ou venait le aVn. J'ai aussi compris que b+λ était la raison. Par contre je ne sais pas comment trouver le (n-p) Auriez vous une piste pour que je puisse trouver (n-p)
donc si je reformule : Vn = Un + λ
donc Vn+1 = Un+1 + λ
= aUn + b + λ
= aVn + b + λ
En utilisant la formule Un = Up (n-p) r
Je trouve : Vn+1 = aVn [(n-p) b + λ ]
J'ai enfin compris (grâce a vous) d'ou venait le aVn. J'ai aussi compris que b+λ était la raison. Par contre je ne sais pas comment trouver le (n-p) Auriez vous une piste pour que je puisse trouver (n-p)
Re: Dm Suite terminale (suite auxiliaire)
inesrMaths a écrit:donc si je reformule : Vn = Un + λ
donc Vn+1 = Un+1 + λ
= aUn + b + λ
= aVn + b + λ
Il y a une erreur à la dernière ligne : tu remplaces
inesrMaths a écrit:En utilisant la formule Un = Up (n-p) r
Je ne sais pas d'où tu sors cette formule mais elle est très certainement fausse.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
