Suite - Suite auxiliaire arithmétique : 1.S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 24 Mai 2013, 18:31
par upium666 » 24 Mai 2013, 18:31
Bonjour à tous et à toutes
Cet exercice a fait l'objet d'une partie d'un DS que je viens de passer il y a quelques heures, et je n'ai eu que quelques minutes pour le faire, malheureusement je l'ai raté :
_{n \in \mathbb{N}} : \left\{\begin{matrix} u_0 = 1 \\ u_{n+1}=\frac{1}{4} u_n + n \ \ (*) \end{matrix}\right.)
1)Déterminer une suite arithmétique
)
qui vérifie la condition : (*)
2)On pose
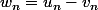
. Montrer que cette suite est géométrique et préciser sa raison
3)Exprimer
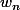
et

en fonction de n
...
Merci de m'aider à me rendre compte que j'ai foiré l'exercice :ptdr:

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 24 Mai 2013, 19:16
par chan79 » 24 Mai 2013, 19:16
upium666 a écrit:Bonjour à tous et à toutes
Cet exercice a fait l'objet d'une partie d'un DS que je viens de passer il y a quelques heures, et je n'ai eu que quelques minutes pour le faire, malheureusement je l'ai raté :
_{n \in \mathbb{N}} : \left\{\begin{matrix} u_0 = 1 \\ u_{n+1}=\frac{1}{4} u_n + n \ \ (*) \end{matrix}\right.)
1)Déterminer une suite arithmétique
)
qui vérifie la condition : (*)
2)On pose
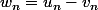
. Montrer que cette suite est géométrique et préciser sa raison
3)Exprimer
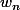
et

en fonction de n
...
Merci de m'aider à me rendre compte que j'ai foiré l'exercice :ptdr:
salut
on pose
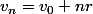
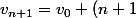r)
il faut que
r=\fra{1}{4}(v_0 +nr)+n)
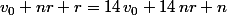
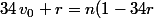)
on peut donc prendre
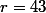
et
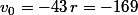
soit
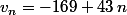
La suite est simple
-
LaCoc6nl
- Membre Naturel
- Messages: 90
- Enregistré le: 29 Mar 2013, 19:06
-
 par LaCoc6nl » 24 Mai 2013, 19:24
par LaCoc6nl » 24 Mai 2013, 19:24
upium666 a écrit:Bonjour à tous et à toutes
Cet exercice a fait l'objet d'une partie d'un DS que je viens de passer il y a quelques heures, et je n'ai eu que quelques minutes pour le faire, malheureusement je l'ai raté :
_{n \in \mathbb{N}} : \left\{\begin{matrix} u_0 = 1 \\ u_{n+1}=\frac{1}{4} u_n + n \ \ (*) \end{matrix}\right.)
1)Déterminer une suite arithmétique
)
qui vérifie la condition : (*)
Ecris :
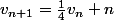
et :
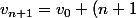* r)
ensuite prouve l'existence de ton

, d'abord arbitraire mais indépendant de

, par identification à partir des premiers termes de la suite ...
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 24 Mai 2013, 20:04
par upium666 » 24 Mai 2013, 20:04
J'ai suivi ce principe dans mon devoir, sauf que contrairement à vous j'ai choisi un

et j'ai déterminé

, cependant ...

s'exprime en fonction de n
J'ai trouvé par exemple :
En choisissant :
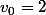
=>
}{3n+4})
Et là j'ai bloqué
Mais j'ai essayé de me ratrapper (même si mon raisonnement ne tient pas ...)
En faisant :

est défini (choisi) n=0
alors
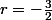
(?!)
ainsi
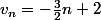
(?!)
(J'ai foiré, je le sens :ptdr: )
Où mon raisonnement ne tient-il pas ?
Et de toute façon ...
Comment peut-on vérifier que notre résultat est juste ? :s))
Merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
