L1 exercice suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Seth
- Membre Naturel
- Messages: 34
- Enregistré le: 13 Oct 2021, 17:14
-
 par Seth » 17 Sep 2022, 13:01
par Seth » 17 Sep 2022, 13:01
Bonjour, j'ai un exercice où je me retrouve bloqué dès la première question et je viens quérir un peu de votre aide pour avancer.
L'énoncé : Soit
_{n\in\mathbb{N}})
une suite strictement positive telle que
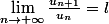
avec

.
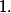
Montrer qu'il existe un entier

tel que pour tout
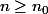
on a

.
J'imagine qu'il faut utiliser la définition de la limite mais je ne vois pas du tout comment je peux m'en servir (comment partir de ça).
Merci d'avance aux personnes qui prendront le temps de me répondre.

-
Decrey
- Messages: 4
- Enregistré le: 17 Sep 2022, 11:20
-
 par Decrey » 17 Sep 2022, 13:26
par Decrey » 17 Sep 2022, 13:26
Bonjour,
En effet, il faut passer par la définition de la limite, en choisissant un epsilon bien précis (dépendant de ta limite l).
Une fois que tu auras écrit ça, tu n'as plus qu'à réarranger (en te rappelant que ta suite est strictement positive), bon courage !
-
Seth
- Membre Naturel
- Messages: 34
- Enregistré le: 13 Oct 2021, 17:14
-
 par Seth » 17 Sep 2022, 13:34
par Seth » 17 Sep 2022, 13:34
D'accord merci ! Donc normalement le

devrait apparaître tout seul ?
-
Decrey
- Messages: 4
- Enregistré le: 17 Sep 2022, 11:20
-
 par Decrey » 17 Sep 2022, 14:20
par Decrey » 17 Sep 2022, 14:20
Pose Vn = (Un+1 / Un) pour résoudre tes ennuis !
-
Seth
- Membre Naturel
- Messages: 34
- Enregistré le: 13 Oct 2021, 17:14
-
 par Seth » 17 Sep 2022, 14:25
par Seth » 17 Sep 2022, 14:25
Bon vraiment je ne vois pas, pourtant ça a l'air simple je suis peut-être trop débile pour le voir, je vais passer cette question ce sera mieux.
Merci en tout cas pour ta réponse Decrey, passe une bonne fin de journée !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités