Suite de cauchy et sa sous suite

[Educ]

Bonjour,

on se place sur un espace vectoriel muni d'une norme

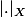
notre objective est de le montrer qu'il est complet pour se faire on doit supposer une suite de Cauchy et de le montrer qu'il est convergente sous la norme

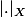
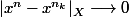
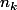
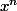
dans la démonstration ils ont fait : quand avec sous suite de qui est une suite de cauchy dans
ma question est ce que on a toujours ça la différence d'une suite de Cauchy avec sa sous suite tend vers zéro

je serais reconnaissant pour tout aide

[Sylviel]

Oui la définition d'une suite de cauchy c'est diam( (u_m)_{m>n}) tends vers 0 (en n). Ce qui signifie en particulier que la différence entre u_n et n'importe quel terme après u_n (donc u_{n_k}) tends vers 0.

[Educ]

un grand merci Sylviel