Dérivées n-ièmes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
sensor
- Membre Naturel
- Messages: 82
- Enregistré le: 08 Nov 2006, 18:52
-
 par sensor » 21 Déc 2006, 19:07
par sensor » 21 Déc 2006, 19:07
Bonjour.
J'ai des exercices sur les dérivées nèmes .
Je pensais que ce serait facile de conjecturer des formules en calculant les 1ers termes mais ce n'est pas le cas.
Mettez moi sur les pistes pour les dérivées nèmes suivantes :
1)y=1/(2x-3)
2)y=1/(ax+b) (avec a R*)
3)y=1/(1-x)²
4)y=(1+x)/(1-x)
5)y=1/(1-x²)
6)y=(sinx)^6 +(cos x)^6+3sin²xcos²x
7)y=exp(2x)cos²x
Merci de me mettre sur les pistes.
(sans faire exprès j'ai mis ce post dans le forum lycée)
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 21 Déc 2006, 19:11
par fahr451 » 21 Déc 2006, 19:11
les 5 premières sont du même genre (après décomposition en éléments simples) :
1/(ax+b) = (ax+b)^(-1) et il suffit de dériver une deux ou trois fois pour voir qu 'il y a du " a" "du factoriel ""du signe un coup - un coup +"
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 21 Déc 2006, 19:12
par Zebulon » 21 Déc 2006, 19:12
Cf mes "belles écritures" dans l'autre
discussion.
Waouw ! J'ai réussi à faire un joli lien ! :we:
-
sensor
- Membre Naturel
- Messages: 82
- Enregistré le: 08 Nov 2006, 18:52
-
 par sensor » 21 Déc 2006, 19:17
par sensor » 21 Déc 2006, 19:17
pouvez vous m'expliquer la décomposition en éléments simples car la prof nous l'a pas éxpliquée...
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 21 Déc 2006, 19:43
par fahr451 » 21 Déc 2006, 19:43
1/(x^2 -1) = a/(x-1) + b/(x+1)
-
sensor
- Membre Naturel
- Messages: 82
- Enregistré le: 08 Nov 2006, 18:52
-
 par sensor » 21 Déc 2006, 19:46
par sensor » 21 Déc 2006, 19:46
mais je ne vois pas trop comment s'y ramener peux tu me corriger une des dérivées pour que je puisse m'en inspirer.
-
sensor
- Membre Naturel
- Messages: 82
- Enregistré le: 08 Nov 2006, 18:52
-
 par sensor » 21 Déc 2006, 20:59
par sensor » 21 Déc 2006, 20:59
merci de m'aider...
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 21 Déc 2006, 21:08
par Zebulon » 21 Déc 2006, 21:08
Je prends le relai puisque Fahr n'est plus connecté.
Qu'est-ce qui te pose problème en fait ? La décomposition en éléments simples ou la dérivée n-ième de

?
-
sensor
- Membre Naturel
- Messages: 82
- Enregistré le: 08 Nov 2006, 18:52
-
 par sensor » 21 Déc 2006, 21:10
par sensor » 21 Déc 2006, 21:10
la décompo en éléments simples
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 21 Déc 2006, 21:18
par Zebulon » 21 Déc 2006, 21:18
OK.
On commence par factoriser le dénominateur :
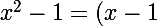(x+1))
donc il existe deux réels a et b tels que

.
Il n'y a plus qu'à déterminer les a et b qui conviennent, par exemple en réduisant au même dénominateur et en identifiant les polynômes du numérateur.
-
sensor
- Membre Naturel
- Messages: 82
- Enregistré le: 08 Nov 2006, 18:52
-
 par sensor » 21 Déc 2006, 21:21
par sensor » 21 Déc 2006, 21:21
je vais le faire pour 1/ax+b et tu me diras si c'est juste.
Attends un peu
-
sensor
- Membre Naturel
- Messages: 82
- Enregistré le: 08 Nov 2006, 18:52
-
 par sensor » 21 Déc 2006, 21:34
par sensor » 21 Déc 2006, 21:34
pour 1/ax+b c simple c (1/a)*(1/(x+(b/a)))
pour 1/(1-x)² c'est a/(1-x) +b/(1+x) ?
Je cherche pour la suite et merci de confirmer
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 21 Déc 2006, 21:37
par Zebulon » 21 Déc 2006, 21:37

est déjà ce qu'on appelle un élément simple.
On veut justement mettre écrire

comme somme d'éléments simples.
Il faut effectivement trouver a et b (les tiens, pas ceux de ax+b qui n'ont rien à voir !)
-
sensor
- Membre Naturel
- Messages: 82
- Enregistré le: 08 Nov 2006, 18:52
-
 par sensor » 21 Déc 2006, 21:49
par sensor » 21 Déc 2006, 21:49
1/x²-1 se décompose en a/x+1 + b/x-1 avec a =1/2 et b=-1/2
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 21 Déc 2006, 21:56
par Zebulon » 21 Déc 2006, 21:56
Si je décompose en
sensor a écrit:1/x²-1 se décompose en a/x+1 + b/x-1
je trouve

et

et pas
a =1/2 et b=-1/2
-
sensor
- Membre Naturel
- Messages: 82
- Enregistré le: 08 Nov 2006, 18:52
-
 par sensor » 21 Déc 2006, 22:01
par sensor » 21 Déc 2006, 22:01
je vais faire les autre décompo
attends
-
sensor
- Membre Naturel
- Messages: 82
- Enregistré le: 08 Nov 2006, 18:52
-
 par sensor » 21 Déc 2006, 22:04
par sensor » 21 Déc 2006, 22:04
pour y=1/(1-x)² je trouve a/(1-x)+(b/1-x) avec a=1/2 et b=1/2
-
sensor
- Membre Naturel
- Messages: 82
- Enregistré le: 08 Nov 2006, 18:52
-
 par sensor » 21 Déc 2006, 22:18
par sensor » 21 Déc 2006, 22:18
comment on fait pour 1/(ax+b) ???
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 21 Déc 2006, 22:23
par Zebulon » 21 Déc 2006, 22:23
Là je quitte, mais j'ai demandé à Sandrine Guillerme de prendre la relève. Elle a accepté, et il faut juste attendre qu'elle finisse un truc.
Bonne soirée et à bientôt !
-
sensor
- Membre Naturel
- Messages: 82
- Enregistré le: 08 Nov 2006, 18:52
-
 par sensor » 21 Déc 2006, 22:24
par sensor » 21 Déc 2006, 22:24
merci pour l'aide
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
