Appellation fonctions

[Florim]

Bonjour,
J'aimerais savoir si les fonctions f tel que soit toujours vérifié ont nom particulier.
Même question avec l'égalité .

Merci d'avance

[lyceen95]

Ton 2ème exemple , il porte un nom connu , classique. Ces fonctions sont les fonctions linéaires.

Si b=0, ça donne f(a+0) = f(a)+f(0) , et donc f(0)=0
Si b=a , ça donne f(a+a) = f(a)+f(a) ...
C'est la définition des fonctions linéaires.

Essayons les mêmes tatonnements avec la première fonction :
si b=0 :
f(a*0) = f(a)* f(0) : Donc f(0)=0, ou alors f est la fonction constante égale à 1
si b=1 :
f(a*1)= f(a)*f(1) : Donc nécéssairement f(1)= 1 , ou f est la fonction constante nulle
Et en fait, les fonctions qui correspondent à cette propriété, ce sont les fonctions de type avec k un réel quelconque. Ou la fonction nulle.

Ce sont toutes les fonctions puissances (avec le problème du 0 ...) , plus la fonction nulle

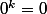
Dans le cas négatif, il faut convenir que pour prolonger la fonction.

[GaBuZoMeu]

Ton 2ème exemple , il porte un nom connu , classique. Ces fonctions sont les fonctions linéaires.

Bonjour,

Je ne serais pas aussi catégorique.
Florim a laissé dans le vague ce qu'il appelle "fonction". On va supposer que c'est de dans . Une fonction linéaire doit aussi vérifier pour tous réels et . Il ne suffit pas d'avoir pour tous réels et .

[Math3matiqu3]

Bonjour,

http://www.les-mathematiques.net/b/e/l/node3.php