Bonjour,
Voilà, j'ai encore un petit problème que je n'arrive pas à résoudre, j'espère que vous pourrez encore m'aider.
On a : E et F sont deux ensembles finis.
card(E)=p
card(F)=n
Soit une fonction de E vers F
Quel est le nombre de fonctions de E vers F ?
Merci d'avance.
PS : C'est la dernière chose qui me manque. Quand j'ai une relation de E vers F, je connais déjà le nombre de relations de E vers F, le nombre d'applications de E vers F, le nombre d'injections de E vers F, le nombre de surjections de E vers F (on m'a renseigné la-dessus) et le nombre de bijections de E vers F.
Quand, je connaîtrai le nombre de fonctions de E vers F, je ne vous embêterai plus avec ça...
Merci d'avance.
Nombre de fonctions
5 messages
- Page 1 sur 1
Bonsoir
Ça donne donc (n+1) possibilités pour chacun des p éléments de E.
Il existe donc p(n+1) fonctions de E vers F.
Dans une fonction de E vers F, chaque élément de E a au plus une image dans F.On a : E et F sont deux ensembles finis.
card(E)=p
card(F)=n
Soit une fonction de E vers F
Quel est le nombre de fonctions de E vers F ?
Ça donne donc (n+1) possibilités pour chacun des p éléments de E.
Il existe donc p(n+1) fonctions de E vers F.
Salut,
Il y a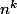 applications d'un ensemble à
applications d'un ensemble à  éléments dans un ensemble à
éléments dans un ensemble à  éléments.
éléments.
Si on appelle fonction de E dans F une application d'une partie de E (l'ensemble de définition) dans F on a
nombre de fonctions de E dans F =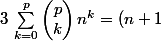^p)
Sauf erreur de ma part.
[modification]
Ps : Une autre façon de voir les choses :
Une fonction de E dans F est une application de E dans F union {non défini}.
On doit peut-être retirer la fonction dont l'ensemble de définition est vide.
Il y a
Si on appelle fonction de E dans F une application d'une partie de E (l'ensemble de définition) dans F on a
nombre de fonctions de E dans F =
Sauf erreur de ma part.
[modification]
Ps : Une autre façon de voir les choses :
Une fonction de E dans F est une application de E dans F union {non défini}.
On doit peut-être retirer la fonction dont l'ensemble de définition est vide.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

 mais de
mais de 