Infinité de solutions
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
emilie943
- Membre Naturel
- Messages: 53
- Enregistré le: 30 Déc 2018, 11:39
-
 par emilie943 » 28 Déc 2020, 16:07
par emilie943 » 28 Déc 2020, 16:07
bonjour
Démontrer qu’il existe une infinité d’entiers

, tels que
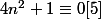
et
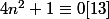
.
J'aimerai avoir quelques pistes.
-
mathelot
 par mathelot » 28 Déc 2020, 16:15
par mathelot » 28 Déc 2020, 16:15
emilie943 a écrit:bonjour
Démontrer qu’il existe une infinité d’entiers

, tels que
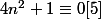
on considère que c'est une équation d'inconnue n , on la résout .
remarque:
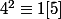
-
emilie943
- Membre Naturel
- Messages: 53
- Enregistré le: 30 Déc 2018, 11:39
-
 par emilie943 » 28 Déc 2020, 16:40
par emilie943 » 28 Déc 2020, 16:40
mais ce n'est pas n qui est au carré ?
-
mathelot
 par mathelot » 28 Déc 2020, 17:21
par mathelot » 28 Déc 2020, 17:21
l'équivalence
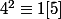
sert dans les calculs; elle indique que 4 possède un inverse , modulo 5.
mais effectivement l'équation est
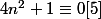
il s'agit de résoudre une équation d'inconnue
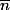
(classe de n modulo 5). on doit aboutir à
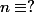
ou
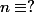
-
emilie943
- Membre Naturel
- Messages: 53
- Enregistré le: 30 Déc 2018, 11:39
-
 par emilie943 » 28 Déc 2020, 23:18
par emilie943 » 28 Déc 2020, 23:18
pour que
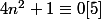
, il faut que
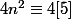
donc
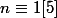
soit
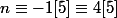
-
mathelot
 par mathelot » 28 Déc 2020, 23:41
par mathelot » 28 Déc 2020, 23:41
-
emilie943
- Membre Naturel
- Messages: 53
- Enregistré le: 30 Déc 2018, 11:39
-
 par emilie943 » 29 Déc 2020, 00:01
par emilie943 » 29 Déc 2020, 00:01
d'accord mon raisonnement est -il tout de même bon ?
-
emilie943
- Membre Naturel
- Messages: 53
- Enregistré le: 30 Déc 2018, 11:39
-
 par emilie943 » 29 Déc 2020, 00:45
par emilie943 » 29 Déc 2020, 00:45
pour
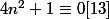
j'ai fait la même méthode et j'ai
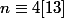
et
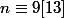
-
mathelot
 par mathelot » 29 Déc 2020, 00:48
par mathelot » 29 Déc 2020, 00:48
oui, tout est exact
du coup, il existe une infinité d'entiers relatifs vérifiant respectivement les équations, tous les entiers qui appartiennent aux classes qui sont solutions.
-
emilie943
- Membre Naturel
- Messages: 53
- Enregistré le: 30 Déc 2018, 11:39
-
 par emilie943 » 29 Déc 2020, 10:22
par emilie943 » 29 Déc 2020, 10:22
super merci beaucoup de votre aide
-
mathelot
 par mathelot » 29 Déc 2020, 12:58
par mathelot » 29 Déc 2020, 12:58
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
, tels que
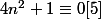
, il faut que
donc
soit