Arithmétique dans Z.

par **hussein** » 14 Nov 2020, 22:33

Bonjour,

Soit l'exercice suivant:
Soit

,

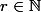
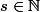
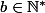
et

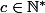
. Déterminer

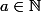
de façon qu'il existe

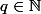
tel que le quotient et le reste de la division de

par

(resp. de

par

) soient

et

(resp.

et

).

Voici la solution que je propose: on doit avoir

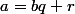
et

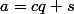
avec

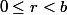
et

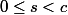
d'où

soit

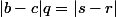
c'est à dire que

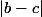
doit diviser

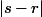
. Mais

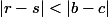
on doit donc avoir

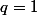
ce qui donne

.

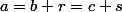
Qu'en pensez-vous ? Ca me parait idiot mais je ne vois rien d'autre.

Merci !

Hussein

par **hussein** » 14 Nov 2020, 22:40

Ah, j'ai fait une erreur, il est faux que

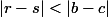
. Du coup je ne vois pas.

par **Sa Majesté** » 15 Nov 2020, 11:07

hussein a écrit:

OK
b, c, r et s sont donnés

par **hussein** » 15 Nov 2020, 11:23

Merci SM.

Donc la condition cest que (b-c) divise (s-r), c'est tout ? Il est idiot cet exo...

par **Sa Majesté** » 15 Nov 2020, 12:23

hussein a écrit:Il est idiot cet exo...

C'est exactement ce que je me suis dit, ou alors j'ai raté un épisode :mrgreen: