Devoir raisonnement par récurrence

[Sayachan]

Bonjours à tous , j'ai vraiment besoins d'aide sur cette exercice que je n'ai pas compris ....

Voici les 4 premiers nombre triangulaire :
T(1)=1
.

T(2)=3
..
.

T(3)=6
...
..
.

T(4)=10
....
...
..
.

1) représenter T(5), T(6) ,T(7).

T(5)=15
.....
....
...
..
.

T(6)=21
......
.....
....
...
..
.
T(7)=28
.......
......
.....
....
...
..
.

2) Exprimer T(n+1) en fonction de T(n)

T(n+1)= T(n)+(n+1)

3) Conjecturer l'expression de 2T(n),puis de T(n) en fonction de n.

Et là je bloque, j'avoue ne pas avoir trop compris la question...

4) valider cette conjecture par un raisonnement par récurrence.

Bon je n'ai pas encore pu essayer cette queqtion mais je risque de bloquer aussi alors si vous pouviez au moins m'exoliquer , j'ai du mal avec les raisonnement par récurrence...


Merci d'avance !

[fatal_error]

Slt,

pour la conjecture,

Pour les T(n), si tu comptes les points et que ces points forment un trinagle rectangle, alors si tu prends 2T(n), tu prends le double de points et ils forment un rectangle (dont l'aire, qui donne le nombre de points, ptet plus simple a calculer)

[Sayachan]

Alors pour commencer merci de ta réponce. Je comprend ce que tu dis mais je ne vois pas en quoi ca va m'aider à conjecturer...

[Lostounet]

Bonjours à tous , j'ai vraiment besoins d'aide sur cette exercice que je n'ai pas compris ....

Voici les 4 premiers nombre triangulaire :
T(1)=1
.

T(2)=3
..
.

T(3)=6
...
..
.

T(4)=10
....
...
..
.

1) représenter T(5), T(6) ,T(7).

T(5)=15
.....
....
...
..
.

T(6)=21
......
.....
....
...
..
.
T(7)=28
.......
......
.....
....
...
..
.

2) Exprimer T(n+1) en fonction de T(n)

T(n+1)= T(n)+(n+1)

3) Conjecturer l'expression de 2T(n),puis de T(n) en fonction de n.

Et là je bloque, j'avoue ne pas avoir trop compris la question...

4) valider cette conjecture par un raisonnement par récurrence.

Bon je n'ai pas encore pu essayer cette queqtion mais je risque de bloquer aussi alors si vous pouviez au moins m'exoliquer , j'ai du mal avec les raisonnement par récurrence...


Merci d'avance !

Salut
Peut-être qu'en dessinant T(n) + T(n+1) comme ça tu verras:



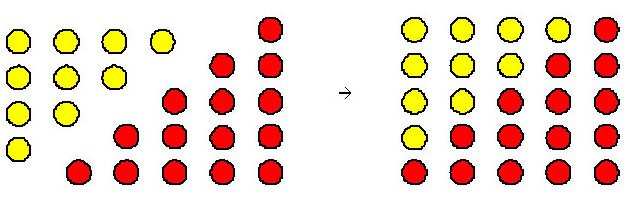
Cette photo montre que (pour n=4)
T(n+1)+T(n)= (n+1)*(n+1)
En effet le total des points c'est le nombre de rangées fois le nombre de points par rangées !

Et tu sais d'après la question d'avant que
T(n+1)=T(n)+(n+1)

Donc finalement en remplaçant dans T(n+1)+T(n)= (n+1)*(n+1) le T(n+1) par T(n)+(n+1) on trouve:

T(n)+(n+1) + T(n) = (n+1) (n+1)

Et donc
2T(n) = ....

[Sayachan]

Merci ppur ta réponce !

Donc si je comprend bien

2T(n)+(n+1)= (n+1)^2
2T(n)=(n+1)^2-(n+1)

[GaBuZoMeu]

Je me souviens qu'en 6e, avec des bâtonnets de bois de largeur 1 et de longueurs 1,2,3,4,.., on faisait ça :



Bon, c'était il y a presque 60 ans.

[beagle]

https://www.didacto.com/35-pedagogie-cuisenaire

waouh les cuisenaire!
ça me rappelle ma jeunesse!
Enfin ma fille je veux dire. j'ai joué à ça avec ma fille.
C'était super ce truc, cela se terminait en jeu de construction.

[Lostounet]

Merci ppur ta réponce !

Donc si je comprend bien

2T(n)+(n+1)= (n+1)^2
2T(n)=(n+1)^2-(n+1)

Exactement
On peut continuer un peu et factoriser:

2T(n)= (n+1) [ (n+1) - 1]

2T(n)= n*(n+1)

Donc T(n)=(n+1)*n/2

Mais ceci reste une conjecture. On l'a vu sur le dessin... Pour n=4

Il faut maintenant essayer de le prouver par récurrencem

[beagle]

euh et pourquoi il faut passer par la récurrence?

en dehors du fait que c'est la question de l'exo.

[Lostounet]

euh et pourquoi il faut passer par la récurrence?

en dehors du fait que c'est la question de l'exo.

Car on a juste vu sur le dessin dans notre raisonnement pour n=4 pour affirmer que T(4)+T(5)=5^2

Après bon ce n'est pas si indispensable ici vu qu'il suffit de compter les points dans un triangle (base*hauteur/2).

Par contre dans d'autres exemples un truc peut marcher pour plein de valeurs de n mais arrête de fonctionner par la suite.

Regarde les intégrales de Borwein par exemple.
Elles valent pi/2 pour tout n jusqu'à 13.

https://en.m.wikipedia.org/wiki/Borwein_integral

Donc on pourrait intuiter que ça vaut toujours pi/2 mais en fait non.

[beagle]

Ben il ya deux méthodes faciles et sympa pour compter ce truc,
celle du carré et une autre...
et qui sont directes,
donc je trouve que c'est dévoyer l'utilité du raisonnement par récurrence que de lui faire démontrer des choses qui passent en direct.
Tout élève perdu dans la jungle (=seul devant sa feuille blanche) devrait ètre capable de retrouver la formule du somme de 1 à n.
par ses propres moyens.

[Lostounet]

Ben il ya deux méthodes faciles et sympa pour compter ce truc,
celle du carré et une autre...
et qui sont directes,
donc je trouve que c'est dévoyer l'utilité du raisonnement par récurrence que de lui faire démontrer des choses qui passent en direct.
Tout élève perdu dans la jungle (=seul devant sa feuille blanche) devrait ètre capable de retrouver la formule du somme de 1 à n.
par ses propres moyens.

Oui.
Peut-être que la philosophie ici est d'apprendre la rédaction ou la démarche de la récurrence sur un exemple le plus basique possible (trouver une formule tout seul et essayer ensuite de la prouver).

Le but n'est sans doute pas de juste trouver la formule en soi.

[Sayachan]

Merci a tous pour vos réponces ! Elles m'ont beaucoup aidées. Donc j'ai essayer de prouver par récurrence:

Supposons que P(n) soit vraie pour un certain rang k tel que 2Tn : n(n+1).
Montrons que k+1 vraie tel que 2T(n+1): (n+1)(n+1+1)= (n+1)(n+2).

Alors oui je n'ai pas vraiment commencé mais je voudrais être sûr d'être sur le bon chemin.....

Donc eb partant de 2T(n) je dois arriver à 2T(n+1) c'est ça ?

[Lostounet]

Merci a tous pour vos réponces ! Elles m'ont beaucoup aidées. Donc j'ai essayer de prouver par récurrence:

Supposons que P(n) soit vraie pour un certain rang k tel que 2Tn : n(n+1).
Montrons que k+1 vraie tel que 2T(n+1): (n+1)(n+1+1)= (n+1)(n+2).

Alors oui je n'ai pas vraiment commencé mais je voudrais être sûr d'être sur le bon chemin.....

Donc eb partant de 2T(n) je dois arriver à 2T(n+1) c'est ça ?

Salut,
Il y a un truc bizarre: tu dis supposons que P(n) soit vraie au rang... k ? On ne voit aucune fois la lettre k dans ton raisonnement.

C'est au rang n que tu as défini P(n) ou alors il faudrait dire supposons P(k) vraie au rang k.


Bref reformulons:
Tu souhaites prouver la proposition P(n) suivante pour tout entier n>=1, nous avons:
T(n)=n(n+1)/2

Initialisation: pour n=1, on a bien T(1)=1*2/2=1

Hérédité: Supposons la propriété vraie au rang n donc supposons que
T(n)=n(n+1)/2 pour un certain rang n.

Le but comme tu sembles bien avoir compris,
C'est justifier que T(n+1)=(n+1)(n+1+1)/2

Pars donc de T(n)=n(n+1)/2
Vois-tu ce qu'on peut ajouter aux deux côtés du signe = pour faire apparaitre à gauche T(n+1) ?

[Sayachan]

T(n+1)=n(n+1)/2 + (n+1) ?

[Sayachan]

T(n+1): n(n+1)/2
T(n+1):n(n+1)/2+(n+1)
T(n+1):(n+1)*(n+1)/2
T(n+1): ((n+1)*(n+1))/2

Je bloque à partir de là... comment arrivé à (n+1)*(n+2) ?

[Lostounet]

T(n+1): n(n+1)/2
T(n+1):n(n+1)/2+(n+1)
T(n+1):(n+1)*(n+1)/2
T(n+1): ((n+1)*(n+1))/2

Je bloque à partir de là... comment arrivé à (n+1)*(n+2) ?

Désolé mais ces lignes n'ont pas de sens pour moi c'est quoi les deux points et tu fais quoi? Tu as mal factorisé.

Tu étais bien parti en écrivant:

T(n+1)=n(n+1)/2 + (n+1)

(Que tu as obtenu en ajoutant (n+1) aux deux côtés)

Maintenant c'est fini: tu dois juste prendre en facteur (n+1)

T(n+1) = (n+1) [n/2 + 1]
= (n+1) (n/2+2/2)
= (n+1)((n+2)/2)
= (n+1)(n+2)/2

Et on a fini l'exercice...

[Sayachan]

Merci pour tous ! Je sias ca fait un petit moment et je viens de me rappeller de ça ... vous m'avee vrailent sauvez la vie merci