Fonction réciproque

[mehdi-128]

Ok merci.

Dans le cas
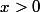
Je trouve

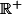
La fonction réalise une bijection de dans

Et là je bloque

[tournesol]

Première remarque :
lorsque x est fixé la fonction Ax est du type K+ arctan .
Il est inutile de dériver pour en connaitre le sens de variation .
tu dois savoir par coeur ( connaissance des fonctions de réferences ) que arctan est strictement croissante . Et l'addition d'une constante ne modifie pas le sens de variations .
Deuxième remarque:
y varie de - infini à + infini et donc Ax(y) varie de arctan(x)-pi/2 à arctan(x)+pi/2 , et en prenant en 1/x la valeur pi/2 si x>0 , et - pi/2 si x<0
Reporte mes indications dans tes tableaux de variations sans oublier que arctan x >0 lorsque x>0 , et que arctan x<0 lorsque x<0

[mehdi-128]

Ok pour les variations de arctan que j'ai étudié je les connais mais j'ai pas compris la fin avec le "en prenant en 1/x la valeur pi/2 si x>0"

J'ai pas compris la logique sur la fin, on en fait quoi des variations de la fonction ?

[tournesol]

Tu as montré que arctan(x)+arctan(1/x)=(signe de x) pi/2
Donc Ax(1/x)=(signe de x) pi/2 , valeur que tu places dans ton tableau de variations .
Par exemple pour x>0 , d'après le tableau des variations , Ax induit une bijection de ]-infini , 1/x[ sur ]arctan(x)-pi/2 ; pi/2[
Or arctan(x)>0 , donc arctan(x)-pi/2 > -pi/2
Donc pour y<1/x on a -pi/2<Ax(y)<pi/2
Si y>1/x , le tableau montre que Ax(y)>pi/2

[mehdi-128]

Je ne comprends rien désolé j'abandonne.

Sans Latex c'est incompréhensible.