Probabilités
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
guillaume100
- Membre Naturel
- Messages: 97
- Enregistré le: 29 Déc 2018, 14:49
-
 par guillaume100 » 04 Fév 2019, 18:24
par guillaume100 » 04 Fév 2019, 18:24
Bonjour à tous,
Soient a>0 et E l'espace des fonctions continues et intégrables de R+ dans R. On norme E par :
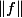
=
}\mid \, \mathrm{d}x \])
Soit
=e^{-ax})
 \, \mathrm{d}x \]) Montrer que
Montrer que  est un endomorphisme continu de E.
est un endomorphisme continu de E.Pour l'endomorphisme ça va dans l'espace des fonctions continues, mais comment montrer que
)
est intégrable ? Il suffit d'utiliser la convergence dominée ?
D'ailleurs, pour la continuité de la fonction, comment montrer que
\leq{K{\| f\|})
?
-
guillaume100
- Membre Naturel
- Messages: 97
- Enregistré le: 29 Déc 2018, 14:49
-
 par guillaume100 » 04 Fév 2019, 18:35
par guillaume100 » 04 Fév 2019, 18:35
D'ailleurs je me suis trompé dans le titre c'est endomorphisme continue
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 04 Fév 2019, 19:18
par infernaleur » 04 Fév 2019, 19:18
Salut,
Il n'y pas que dans le titre où tu t'es trompé ^^
Si je suis ce que tu as écris déjà on a à gauche un élément de E et à droite un réel, il y a déjà un problème, et pour les dx et dt fait attention parce que avec ce que tu as écris on a
=e^{-ax}e^{at}f(t)x)
même si on ne sait pas qui sont x et t .... (bref c'est faux ton truc)
Mais bon on devine quand même que c'est plutôt :
(x)=e^{-ax}\int_{0}^{x}{e^{at}f(t)dt})
Pour montrer que ce qui est au dessus est intégrable, t'as juste à faire rentrer l’exponentielle dans l'intégrale et comme dans ton intégrale t varie de 0 à x et que a est positif, l'exponentielle sera plus petite que 1.
-
guillaume100
- Membre Naturel
- Messages: 97
- Enregistré le: 29 Déc 2018, 14:49
-
 par guillaume100 » 04 Fév 2019, 20:10
par guillaume100 » 04 Fév 2019, 20:10
Merci pour la réponse !
Ouais je me suis trompé.
Concernant la continuité, quel théorème utiliser pour échanger les intégrales ? (si il faut les échanger)
-
aviateur
 par aviateur » 05 Fév 2019, 01:25
par aviateur » 05 Fév 2019, 01:25
infernaleur a écrit:Pour montrer que ce qui est au dessus est intégrable, t'as juste à faire rentrer l’exponentielle dans l'intégrale et comme dans ton intégrale t varie de 0 à x et que a est positif, l'exponentielle sera plus petite que 1.
Bonjour ça c'est vrai i.e on a
(x)|\leq \int_ 0^x |f(t) | dt.)
Mais en quoi cela prouve que
)
est intégrable?
Cela montre que
)
est bornée (car
(x)|\leq \int_ 0^\infty |f(t) | dt=||f||.)
) et c'est tout.
La réponse est moins évidente que ça. C'est à dire qu'il faut montrer que
(x)| dx <\infty)
(et même un peu plus que ça vu qu'on veut la continuité).
Cela ne veut pas dire que c'est vraiment compliqué mais il faut d'abord savoir ce qu'il faut démontrer.
Ceci étant dit je suis d'accord avec @infernaleur qu'il faille bien écrire les choses, i.e commencer par faire l'amalgame entre une fonction et les valeurs prises par la fonction, c'est pas très jojo.
-
guillaume100
- Membre Naturel
- Messages: 97
- Enregistré le: 29 Déc 2018, 14:49
-
 par guillaume100 » 05 Fév 2019, 13:40
par guillaume100 » 05 Fév 2019, 13:40
Salut,
Merci pour la réponse @aviateur, là quand j'essaye de majorer la double intégrale, j'utilise l'inégalité de Cauchy-Schwarz sur la deuxième (celle qui va de 0à x) mais ça mène à une intégrale non convergente, tu peux me donner un indice stp ?
-
aviateur
 par aviateur » 05 Fév 2019, 17:42
par aviateur » 05 Fév 2019, 17:42
Bonjour
Oui je ne voulais pas donner la solution avant d'être sûr que tu ais bien compris la question.
En effet comme on te l'a fait remarquer
)
et
(x))
c'est pas la même chose.
Mais surtout, ensuite quand tu dis je veux montrer que
\leq K ||f||)
et bien cela n'a pas de sens.
Cela laisse un doute, est-ce que c'est des erreurs de frappes (mais bon ) ou alors ??.
Alors je ne te donne pas la solution mais simplement pour montrer l'intégrabilité de
)
et l'estimation recherchée (qu'il te reste à bien écrire) il faut utiliser le théorème de Fubini, c'est à dire échanger les deux ordres d'intégration. A savoir qu'il y a une petite difficulté technique.
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 05 Fév 2019, 19:45
par infernaleur » 05 Fév 2019, 19:45
Merci pour la correction Aviateur j'avais effectivement écrit n'importe quoi ^^
-
aviateur
 par aviateur » 05 Fév 2019, 19:48
par aviateur » 05 Fév 2019, 19:48
@infernaleur, Pas vraiment parce que avant tout, il faut bien faire remarquer que l'écriture des questions doit avoir un sens et c'est ce que tu as fait.
-
guillaume100
- Membre Naturel
- Messages: 97
- Enregistré le: 29 Déc 2018, 14:49
-
 par guillaume100 » 06 Fév 2019, 16:54
par guillaume100 » 06 Fév 2019, 16:54
Bonjour, merci pour l'explication aviateur,
Mais
\| \leq K\| f\|)
ça du sens c'est que la norme de l'endomorphisme
)
est inférieure à une constante K fois celle de

non ?; ça a pas de sens si je pars de ma définition où j'ai écrit
)
au lieu de
(x))
; c'est des fautes de frappes ouais haha ! Enfin je confondrais plus f(x) et f
Le théorème de Fubini il dit que si la double intégrale de la valeur absolue converge alors on peut échanger les intégrales, mais là la double intégrale de la valeur absolue elle converge pas forcément (la première intégrale ouais mais pas la deuxième), vous auriez un indice svp ??
-
aviateur
 par aviateur » 06 Fév 2019, 17:49
par aviateur » 06 Fév 2019, 17:49
Bonjour Ici tu mets une norme à
)
mais dans la question non.!! C'est de ça qu'on avait parlé.
Concernant la démo
On a
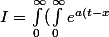} |f(t)| 1_{[0,x]}(t) dx) dt =\int_0^\infty |f(t)| ( \int_t ^\infty e^{a(t-x)} dx) dt =\dfrac{1}{a} \int_0^\infty |f(t)| dt =\dfrac{1}{a} ||f|| <\infty)
(par hypothèses sur f)
On peut alors appliquer Fubini d'où
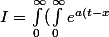} |f(t)| 1_{[0,x]}(t) dt) dx=\int_0^\infty ( \int_0 ^x e^{a(t-x)} |f(t)| dt) dx=\int_0^\infty |\phi(f)(x)| dx = \dfrac{1}{a} ||f|| .)
Or
(x)| dx =\int_0^\infty |\int_0 ^x e^{a(t-x)} f(t) dt | dx\leq \int_0^\infty \int_0 ^x e^{a(t-x)} |f(t)| dt dx = I= \dfrac{1}{a} ||f||)
Ce qui donne à la fois l'intégrabilité et l'estimation recherchée.
-
guillaume100
- Membre Naturel
- Messages: 97
- Enregistré le: 29 Déc 2018, 14:49
-
 par guillaume100 » 06 Fév 2019, 21:06
par guillaume100 » 06 Fév 2019, 21:06
Ah ouais cimer @aviateur !
J'avais pas vu aussi que j'avais oublié la norme mais je m'en souviendrai, et aussi du fait de se servir à la base de la double intégrale que l'on veut avoir et pas en partant de la première intégrale !
-
aviateur
 par aviateur » 06 Fév 2019, 21:20
par aviateur » 06 Fév 2019, 21:20
Une question tout à fait importante par rapport à cet exo. L'espace E muni de cette norme est-il complet?
-
guillaume100
- Membre Naturel
- Messages: 97
- Enregistré le: 29 Déc 2018, 14:49
-
 par guillaume100 » 07 Fév 2019, 16:07
par guillaume100 » 07 Fév 2019, 16:07
C'est plus à notre programme les espaces complets et les suites de Cauchy mais si fn est une suite qui tend vers f au sens de Cauchy, il s'agit de montrer que f est intégrable
-f_q(t)\mid dt}\leq \epsilon)
Là je remplace fp par f mais j'arrive pas à obtenir la convergence uniforme de fn sur f, j'ai loupé un truc ?
-
aviateur
 par aviateur » 07 Fév 2019, 18:13
par aviateur » 07 Fév 2019, 18:13
Bonjour
Quand tu dis ce n'est plus au programme (de quoi d'ailleurs?), c'est un peu bizarre, en tout cas j'en suis très étonné . En effet on ne travaille bien que dans les espaces complets.
En particulier

est complet .
De toute façon si c'est pas au programme, rien n'empêche de poser la question.
Dans

on sait ce que c'est une suite de Cauchy. Donc on n'a pas de problème de savoir ce qu'est une suite de Cauchy dans (E,|| ||). Une suite de Cauchy converge-t-elle dans E?
En plus certaines choses m'intriguent. En effet dans ta question tu a parlé de fonction intégrable, on a aussi utilisé Fubini et dixit espace complet? (vraiment je ne comprends plus rien) . Voir tout ça sans savoir ce qu'est un espace complet!
-
guillaume100
- Membre Naturel
- Messages: 97
- Enregistré le: 29 Déc 2018, 14:49
-
 par guillaume100 » 07 Fév 2019, 22:49
par guillaume100 » 07 Fév 2019, 22:49
Merci pour la réponse,
Une suite de Cauchy converge dans E car si elle divergeait alors elle ne serait plus intégrable au bout d'un certain temps et si elle admet deux points d'adhérence on peut extraire une une fonction
})
et une fonction
})
, et en faisant l'intégrale de la valeur absolue de leur différence en passant à la limite (mais je sais pas comment faire passer la limite dans l'intégrale) alors l'intégrale diverge ce qui est contraire aux suites de Cauchy.
Donc les suites de Cauchy convergent, mais est-ce que elles convergent dans E ? Si elle converge vers f, et que f n'était pas intégrable, alors la suite est pas de Cauchy parce que si j'utilise l'inégalité triangulaire dans l'intégrale que j'avais écrite tout à l'heure (en remplaçant fp par f) alors j'ai un intégrale divergente et après je bloque haha
-Non c'est plus au programme depuis 2014 les suites de Cauchy et les espaces complets en spé MP mais ça m'intéresse de savoir quand même !
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 08 Fév 2019, 02:24
par LB2 » 08 Fév 2019, 02:24
Effectivement et c'est assez fou quand même car comment parler de topologie dans les espaces vectoriels normés sans parler d'espaces complets... Sans parler de l'étude des séries : absolue convergence => convergence, critère de Cauchy...
A mon époque, pas si lointaine mon professeur étant passionné de topologie, on avait fait les espaces métriques en cours, la compacité (Borel-Lebesgue, précompact+complet => compact), et les espaces séparables en DM...
-
aviateur
 par aviateur » 08 Fév 2019, 16:56
par aviateur » 08 Fév 2019, 16:56
Bonjour
Je reviens sur cet exercice avec commentaires et questions intéressant qu'il soulève
1. D'abord le titre pourquoi probabilités?
2. Si on considère la suites de fonctions
)
affines par morceaux et continues définies par
=1)
sur [0,1] ,
= -n x+n +1)
sur
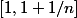
=0)
sur
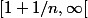
La suite (f_n) est de Cauchy. Converge-t-elle dans E?
3. Enfin l'opérateur continu défini sur E

à un effet régularisant.
Comme par exemple les fonctions
)
précédentes sont continues mais pas dérivables.
En exercice on peut montrer que les images
)
sont dérivables.
Et puis la suite
)
converge-t-elle (dans E)?
-
guillaume100
- Membre Naturel
- Messages: 97
- Enregistré le: 29 Déc 2018, 14:49
-
 par guillaume100 » 08 Fév 2019, 20:32
par guillaume100 » 08 Fév 2019, 20:32
Salut merci pour vos réponses !
-LB2: on a vu que la convergence absolue implique la convergence parce que on travaille que dans des espaces complets je crois
-aviateur: le titre je me suis trompé c'est plutôt "endomorphisme continu"; la suite

converge vers la fonction qui vaut 1 sur [0,1] et 0 sur
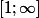
, elle est intégrable sur R+ mais pas continue donc appartient pas à E et les

ne convergent pas dans E. Quand je calcule
)
, j'obtiens
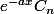
où

est une constante qui dépend de n, donc elle est dérivable, et intégrable, car quand on calcule la limite de

, on obtient
-1/a)
et
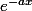
fois cette constante est intégrable sur R+
-
aviateur
 par aviateur » 09 Fév 2019, 06:03
par aviateur » 09 Fév 2019, 06:03
Bonjour
Dans ta réponse du 7 février tu donne exactement la bonne définition d'une suite de Cauchy dans E.
Alors concernant la suite (f_n), la réponse précise consiste à calculer la norme de. f_n- f_p et de vérifier que c'est bien une suite Cauchy. C'est un peu de calculs. Ensuite le raisonnement est le suivant c, est de supposer que si la suite converge alors nécessairement la limite f c'est la fonction que tu donne mais f n'est pas dans E, (la conséquence c'est que E n'est pas complet,
Concernant l'image de la suite f_n par phi je ne suis pas d'accord avec ton calcul (il faut considérer 3 cas
x est entre 0 et 1
x est entre 1 et 1+1/n
x est plus grand que 1+1/n
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
